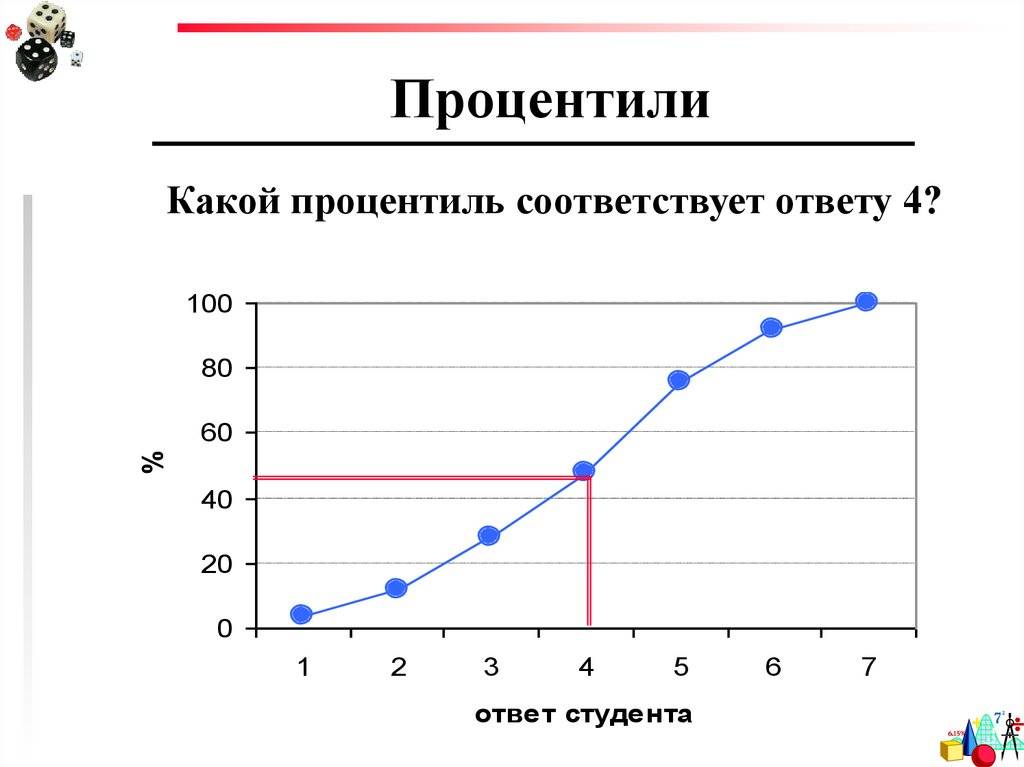
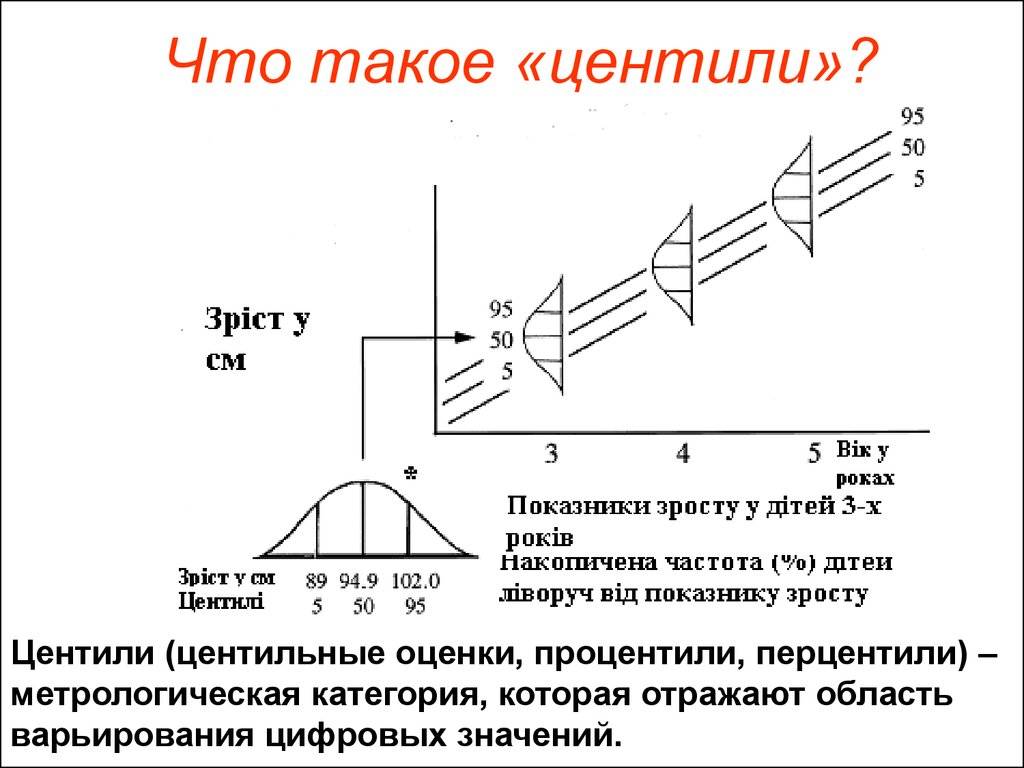
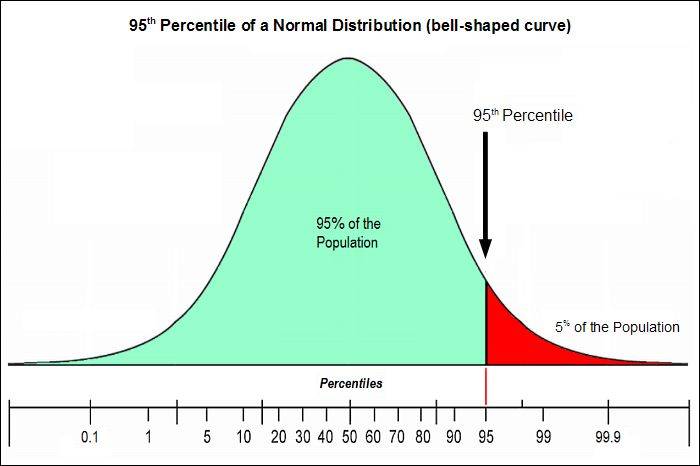
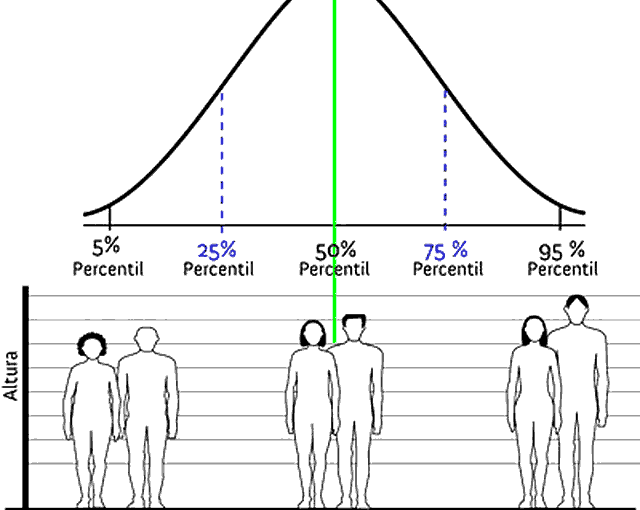
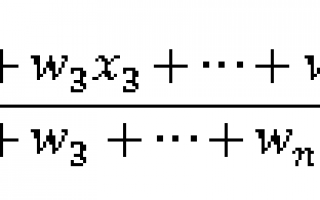Как посчитать процентиль по формуле персентиль в excel

Определение

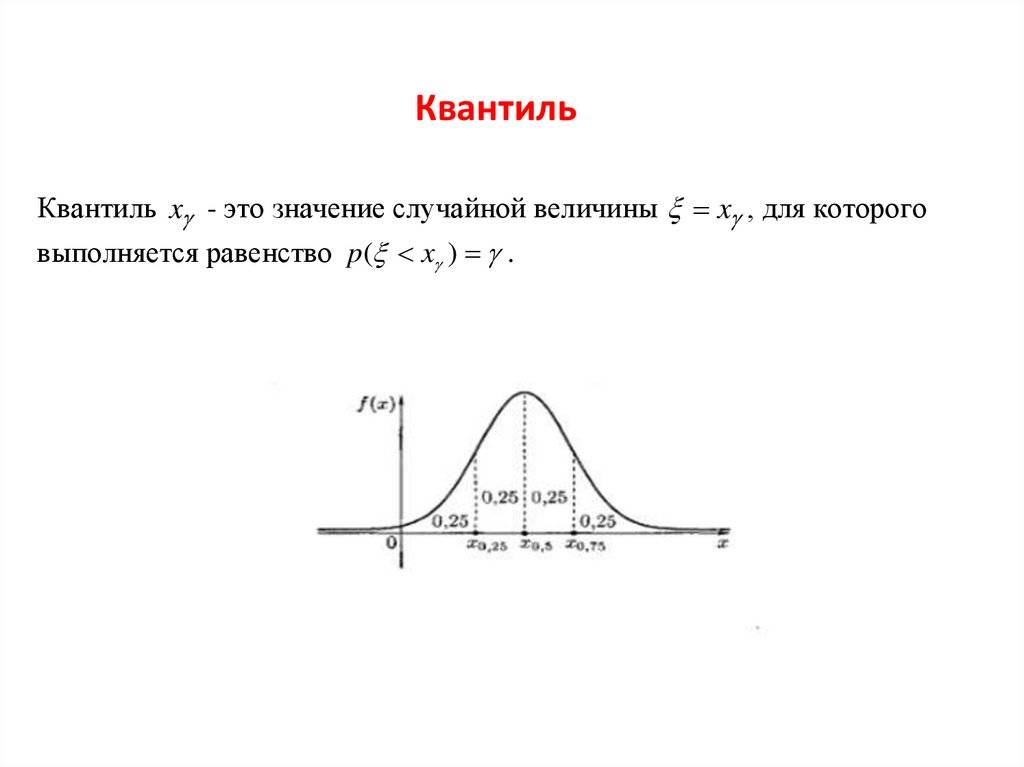
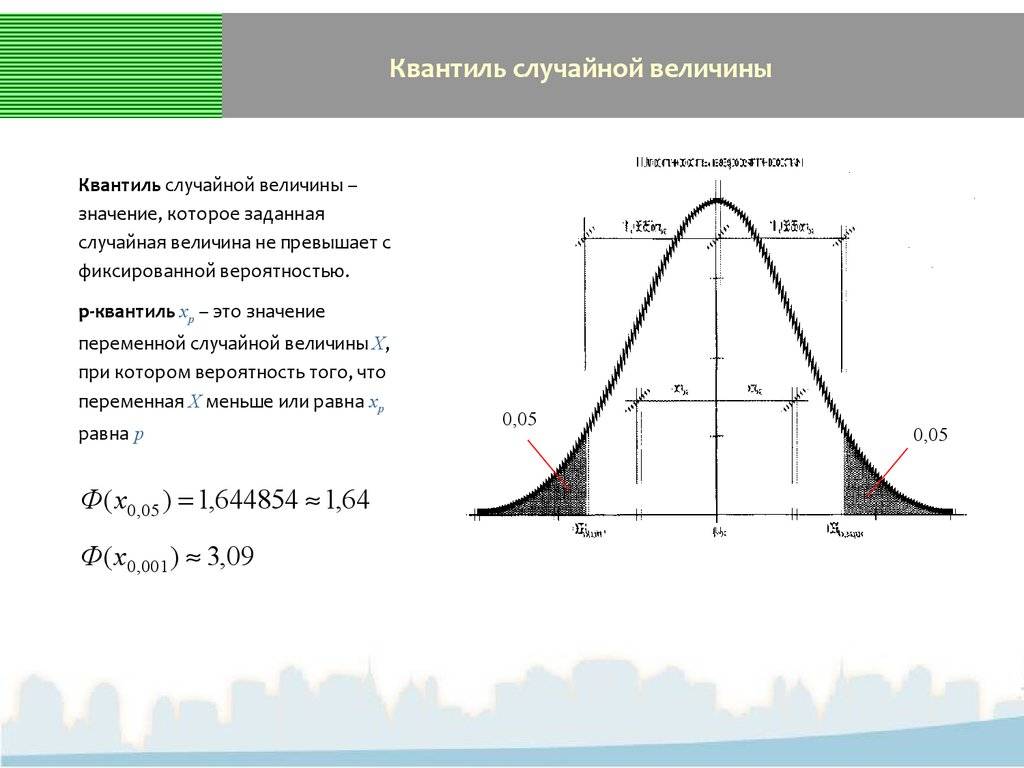
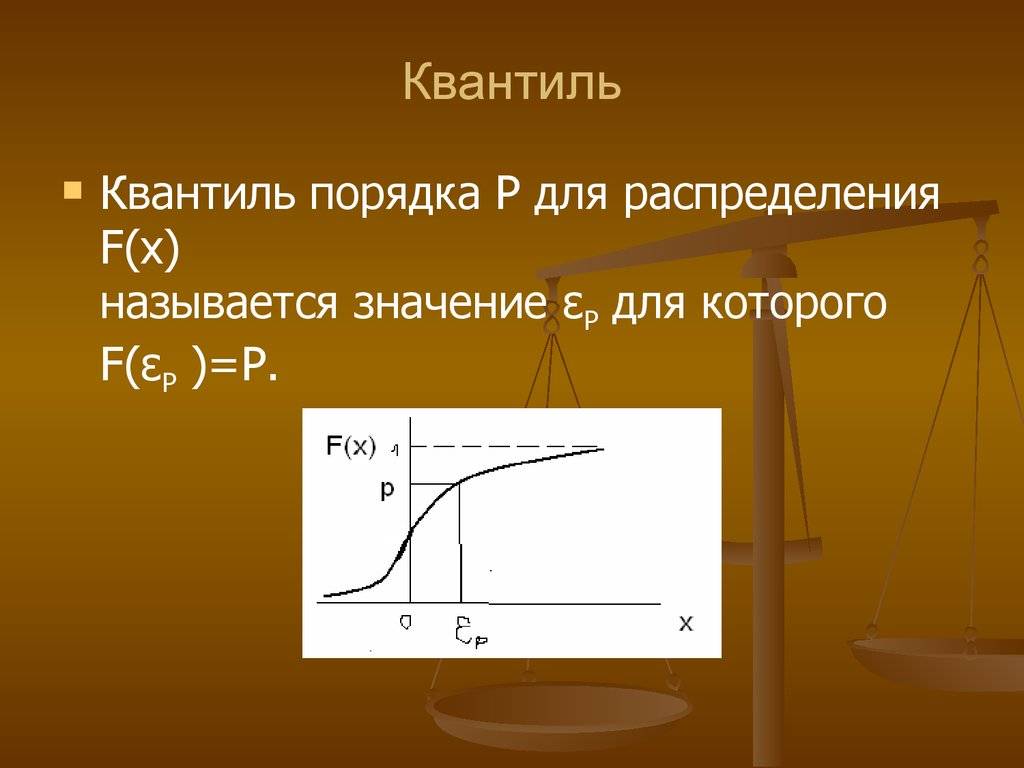
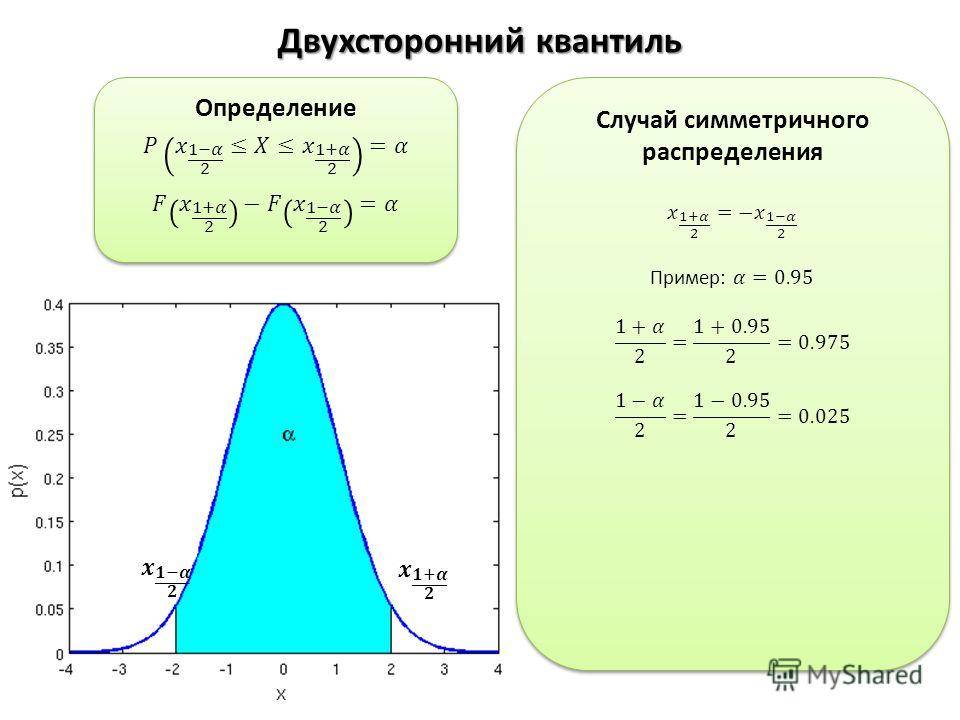
Рассмотрим вероятностное пространство (Ω,F,P){\displaystyle (\Omega ,\;{\mathcal {F}},\;\mathbb {P} )} и PX{\displaystyle \mathbb {P} ^{X}} — вероятностная мера, задающая распределение некоторой случайной величины X{\displaystyle X}. Пусть фиксировано α∈(,1){\displaystyle \alpha \in (0,\;1)}. Тогда α{\displaystyle \alpha }-квантилем (или квантилем уровня α{\displaystyle \alpha }) распределения PX{\displaystyle \mathbb {P} ^{X}} называется число xα∈R{\displaystyle x_{\alpha }\in \mathbb {R} }, такое что

P(X⩽xα)⩾α{\displaystyle \mathbb {P} (X\leqslant x_{\alpha })\geqslant \alpha } ,

P(X⩾xα)⩾1−α.{\displaystyle \mathbb {P} (X\geqslant x_{\alpha })\geqslant 1-\alpha .}

В некоторых источниках (например, в англоязычной литературе) k{\displaystyle k}-м q{\displaystyle q}-квантилем называется квантиль уровня kq{\displaystyle k/q}, то есть (kq){\displaystyle (k/q)}-квантиль в предыдущих обозначениях.

Медиана и квартили

Квантили нормального распределения

Основная статья: Медиана (статистика)

0,25-квантиль называется первым (или нижним) кварти́лем (от лат. quarta — четверть);
0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым кварти́лем;
0,75-квантиль называется третьим (или верхним) кварти́лем.

Интеркварти́льным размахом (англ. Interquartile range) называется разность между третьим и первым квартилями, то есть x,75−x,25{\displaystyle x_{0{,}75}-x_{0{,}25}}. Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.

Что такое усреднение?

Усреднение — это постепенное наращивание позиции в трейдинге частями, чтобы быстрее выйти из убытков либо увеличить прибыль.

На словах объяснять этот термин бесполезно, гораздо эффективнее будет сразу взглянуть на график.

Нажмите, чтобы увеличить.

Как видите, сначала мы вошли в первую сделку на продажу по золоту, и рынок пошел против нас. В надежде, что ситуация изменится, была открыта еще одна позиция, чтобы быстрее выйти из убытка. Далее, аналогичным образом третья и т.д. Таких сделок может быть бесконечно много.

В результате, когда рынок хотя бы немного пошел в нашу сторону, мы просто закрываем все позиции в плюс и получаем прибыль.

Взвешенное среднее

Взвешенное среднее используют тогда, когда некоторые значения интересующей нас переменной x более важны, чем другие

Мы присоединяем вес wi к каждому из значений xi в нашей выборке для того, чтобы учесть эту важность

Если значения x₁, x₂ … x_n имеют соответствующий вес w₁, w₂ … w_n, то взвешенное арифметическое среднее выглядит следующим образом:

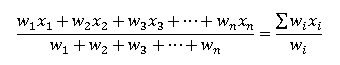
Например, предположим, что мы заинтересованы в определении средней продолжительности госпитализации в каком-либо районе и знаем средний реабилитационный период больных в каждой больнице. Учитываем количество информации, в первом приближении принимая за вес каждого наблюдения число больных в больнице.

Взвешенное среднее и среднее арифметическое идентичны, если каждый вес равен единице.

Определение

—кванти́ль
случайной величины с функцией распределения
— это
любое число удовлетворяющее двум условиям:

Заметим, что данные условия эквивалентны следующим:

Если — непрерывная строго монотонная функция, то
существует единственный квантиль
любого порядка который
однозначно определяется из уравнения
и, следовательно,
выражается через функцию, обратную к функции распределения:

Кроме указанной ситуации, когда уравнение имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:

если указанное уравнение не имеет решений, то это означает, что существует единственная точка в которой функция распределения имеет разрыв, которая удовлетворяет данному определению и является квантилем порядка . Для этой точки выполнены соотношения: и (первое неравенство строгое, а второе может быть как строгим, так и обращаться в равенство).
если уравнение имеет более одного решения, то все его решения образуют интервал, на котором функция распределения постоянна. В качестве квантиля порядка может быть взята любая точка этого интервала. Содержательные выводы, в которых участвует квантиль, от этого существенно не изменятся, поскольку вероятность попадания случайной величины в данный интервал равна нулю.

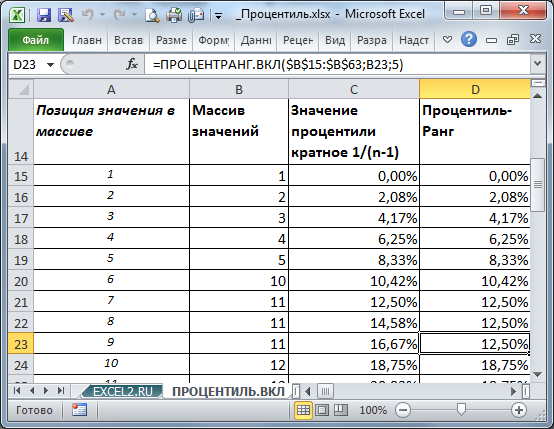
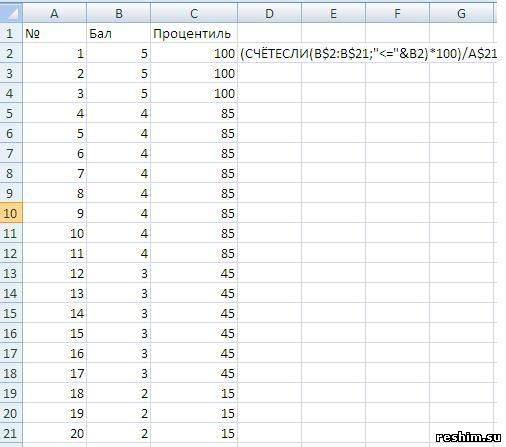
Пример вычисления формулы процентиля в Excel

Перцентили (они же процентили или персентили) часто применяются в анализе данных. Они являются инструментом для оценки результатов на фоне целой группы данных. С их помощью можно, например, определить персентильную классификацию работника по его годовому обороту.

В программе Excel персентильную классификацию можно легко определить при использовании функции ПЕРСЕНТИЛЬ. Данная функция имеет 2 аргументы:

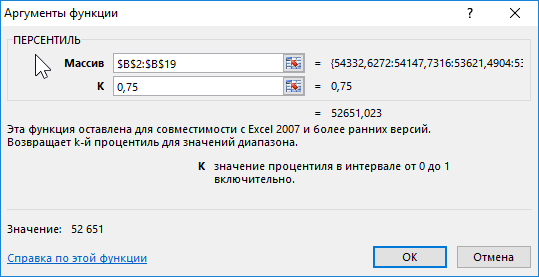
Массив – диапазон исходных данных.
К – значение найденного процентиля (чаще всего число в десятичной дроби диапазоном от 0 и до 1).

В примере, изображенном ниже на рисунке ячейка D6 содержит значение, которое является результатом вычисления ниже указанной формулы – число 0,75 процентиля данных диапазоне ячеек $B$2:$B$19:

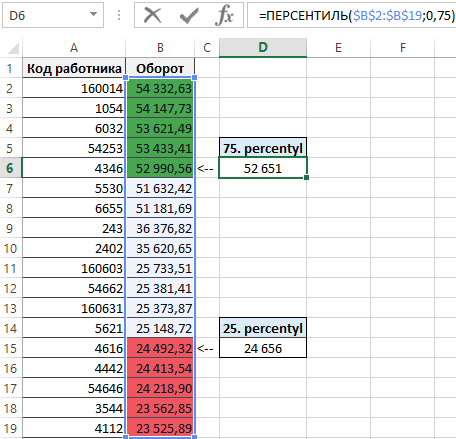
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовые обороты превышают 52651 работает лучше, чем 75% всех остальных сотрудников.

Ячейка D15 содержит результат вычисления формулы, которая возвращает число 25 процентиля данных в диапазоне ячеек $B$2:$B$19.

Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовой оборот не превышает 24656 находится среди 25% самых слабых сотрудников.

В данном примере используется условное форматирование использующие выше приведенные значения перцентилей. Значения больше чем 75 перцентиля выделены зеленым цветом, а значения меньше чем 25 перцентиля выделены красным цветом.

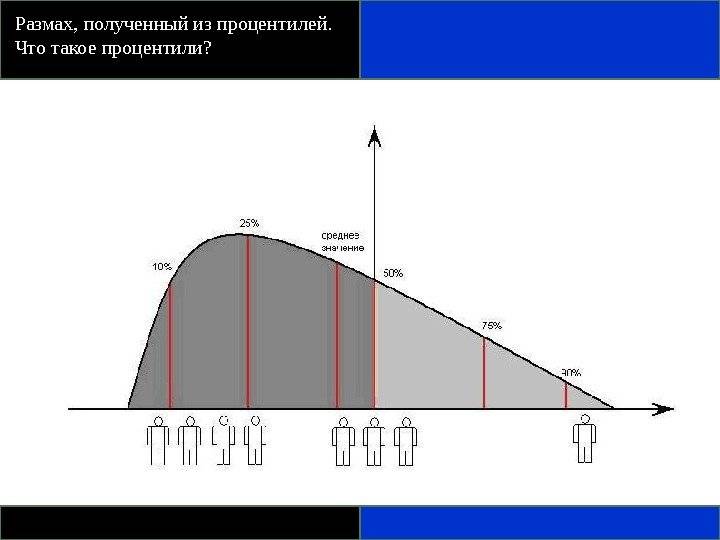
Размах, полученный из процентилей

Что такое процентили

Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины переменной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.

Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.

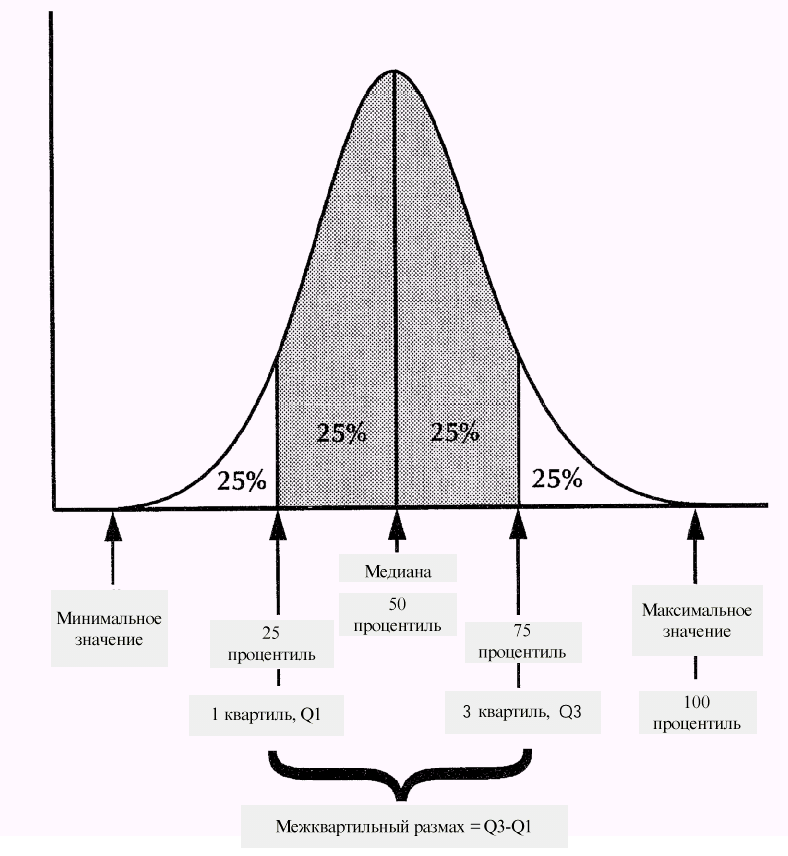
Величины X, которые делят упорядоченный набор значений на 10 равных групп, т. е. 10-й, 20-й, 30-й,…, 90 и процентили, называются децилями. Величины X, которые делят упорядоченный набор значений на 4 равные группы, т.е. 25-й, 50-й и 75-й процентили, называются квартилями. 50-й процентиль — это медиана.

Применение процентилей

Мы можем добиться такой формы описания рассеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.

Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.

Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблюдения, которые располагаются между 10-м и 90-м процентилями.

Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.

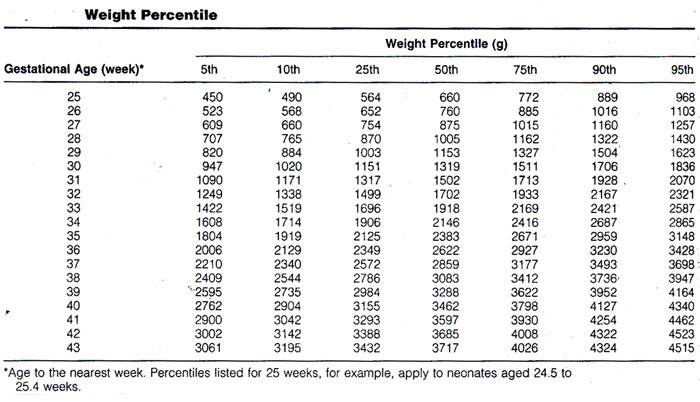
Примеры вычисления процентилей

Рассмотрим для примера набор данных из N = 12 значений, представленный ниже в таблице 1. Для этого набора данных мы рассчитаем 40-й процентиль с помощью всех трех описанных выше методов. Значения набора данных упорядочены по величине от меньших к большим и каждому из них присвоен ранг от 1 до 12. Мы выполним расчет по трем определениям и сравним результаты наших расчетов.

Таблица 1. Набор данных для примера расчетов

Значение	Ранг
2	1
4	2
8	3
9	4
11	5
13	6
15	7
17	8
20	9
24	10
29	11
30	12

Расчет по методу 1

Определяем порядковый ранг n по определению 1 для 40-го процентиля:

Поскольку порядковый ранг n не является целым числом, мы округляем его до n = 5. По таблице 1, значение 40-го процентиля для n = 5 равно 11.

Расчет по методу 2

Этот метод является альтернативой методу ближайшего ранга. В нем используется линейная интерполяция между соседними значениями в наборе данных. Дробный порядковый номер x рассчитывается по следующей формуле:

Порядковый ранг n = 5. Дробная часть {x} = 0,4 результата вычисления дробного порядкового номера x затем используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером v_n и следующего за ним большего значения v_n+1:

Расчет по методу 3

Этот метод является еще одной альтернативой методу ближайшего ранга. В нем используется линейная интерполяция между соседними значениями в наборе данных. Определяем дробный порядковый номер x:

Порядковый ранг n = 5. Дробная часть {x} = 0,2 результата вычисления дробного порядкового номера x затем используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером v_n и следующего за ним большего значения v_n+1:

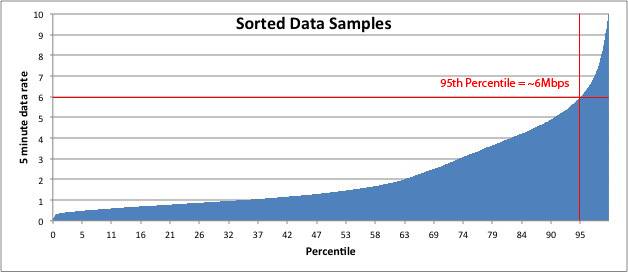
Метод оплаты по 95-му процентилю является стандартным промышленным методом измерения ширины полосы пропускания (пропускной способности) канала, используемым интернет-провайдерами и дата-центрами.

Среднее геометрическое

При несимметричном распределении данных среднее арифметическое не будет обобщающим показателем распределения.

Если данные скошены вправо, то можно создать более симметричное распределение, если взять логарифм (по основанию 10 или по основанию е) каждого значения переменной в наборе данных. Среднее арифметическое значений этих логарифмов — характеристика распределения для преобразованных данных.

Чтобы получить меру с теми же единицами измерения, что и первоначальные наблюдения, нужно осуществить обратное преобразование — потенцирование (т. е. взять антилогарифм) средней логарифмированных данных; мы называем такую величину среднее геометрическое.

Если распределение данных логарифма приблизительно симметричное, то среднее геометрическое подобно медиане и меньше, чем среднее необработанных данных.

Усреднение стоимости

Одной из стратегий, которая начала завоевывать популярность в последнее время, является усреднение стоимости (Value Averaging). Придумал ее Майкл Эдельсон в начале 1990-х годов. Направлена она на то, чтобы инвестировать больше, когда цена на акции падает, и меньше, когда эта цена растет. Сравнение стратегий приведено в таблице ниже:

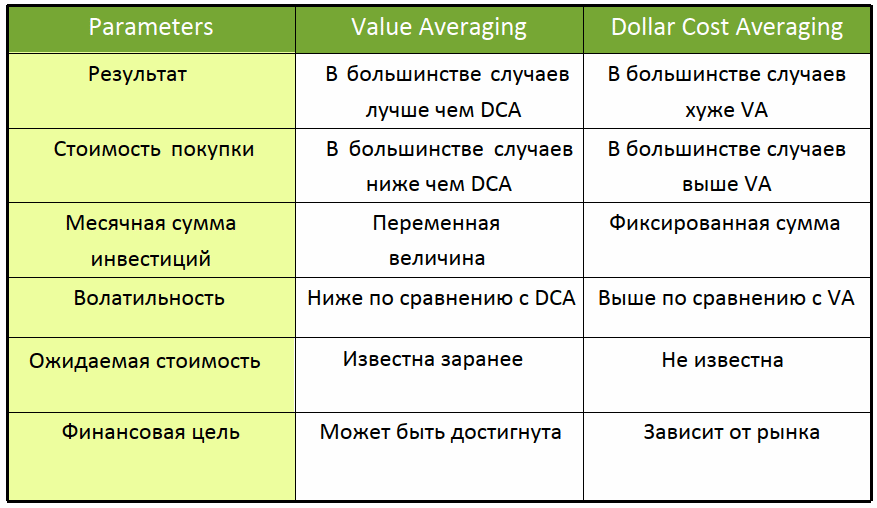
Два примера ниже помогут понять смысл стратегии усреднения стоимости. Первый вариант:

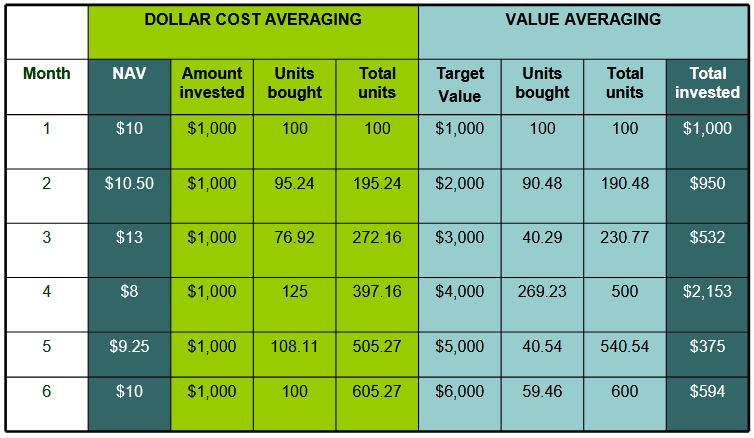
В этом примере у нас есть произвольная акция по начальной цене (NAV) 10 долларов. В течение полугода мы инвестируем в нее двумя методами: DCA и VA. Через полгода цена возвращается к прежнему значению.

В первом случае мы каждый месяц закупаем актив по рыночной цене на сумму 1000$. Units bought = количество купленных единиц (акций) в данном месяце. Первая строка одинакова для обоих методов: на 1000$ покупается 100 акций. Total units = общее число купленных акций.

Различия начинаются дальше — во второй месяц актив немного вырос и его цена составило 10.5$. По методу DCA мы снова использовали для покупки 1000$ и на этот купили меньше, чем 100 акций (а именно 95.24). Для простоты считаем возможным купить дробное число.

А вот по методу VA мы считаем, что наша целевая стоимость должна составлять не менее 2000$, которые составляют два взноса DCA. Как посчитать новый взнос? Рыночная цена у нас 10.5$ плюс 100 купленных в прошлом месяце акций. Общая стоимость равна 10.5 × 100 = 1050 долларов, т.е. нам нужно докупить актив на сумму 2000 – 1050 = 950$. Или 90.48 акции.

В третий месяц с целевой стоимостью 3000$ следует довольно резкий рост цены акции до 13$ и мы видим большую разницу в подходах: по DCA мы по-прежнему закупаемся на 1000$, зато по VA только на 532, т.е. на сумму почти в два раза меньше. Что неудивительно: актив в рамках подхода стал весьма дорогим. Зато когда в четвертый месяц цена сильно падает до 8 долларов, мы наоборот тратим на покупку по VA в два раза больше: а именно 2153$. Итог:

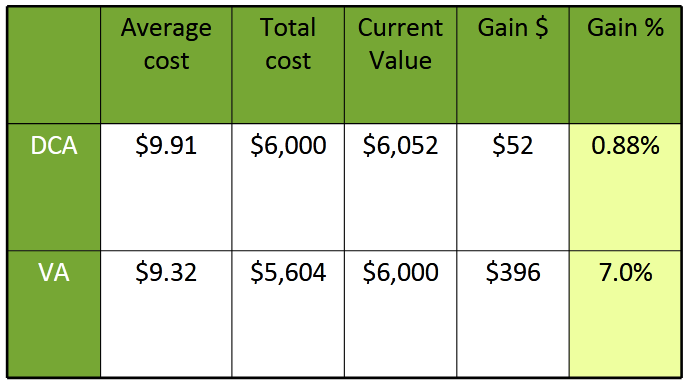
В результате по методу VA мы потратили почти на 400$ меньше, чем по DCA (5604$), получив прибыль в 7% вместо 0.88% по DCA. Почему это произошло? Мы покупали больше акций по низким ценам и меньше по высоким, причем в отличие от спекулянтов нам не пришлось угадывать локальные минимумы и максимумы. Кстати, при очень резком росте цены усреднение стоимости может даже потребовать продажи части акций, чтобы вернуться с целевому уровню — но такое бывает редко.

Теперь обратимся к реальному рынку США и протестируем метод на годовом отрезке с помесячным внесением средств:

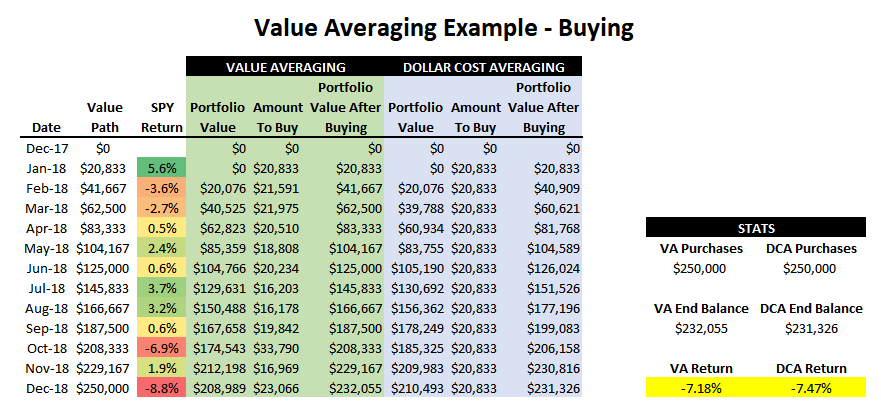
Здесь рассмотрены инвестиции в фонд SPY, отслеживающий индекс S&P500. В случае метода DCA инвестируется 250 тысяч долларов, что при ежемесячном вкладе соответствует 20 833$. В случае метода VA целевая стоимость портфеля составляет 20 833, умноженная на номер месяца. Т.е. в феврале она равна 20 833 × 2 = 41 667, в марте 20 833 × 3 = 62 500 и т.д.

В самом конце года рынок сильно упал и годовой результат оказался отрицательным. Тем не менее по методу VA убыток составил 7.18%, тогда как по DCA минус 7.47%. Иначе говоря, VA дал преимущество в 0.3%. Немного, но на дистанции в 10 лет это 3% дохода.

Согласно расчетам Эдельсона, на дистанции 1926-2005 гг. стратегия DCA на рынке США дала бы 11.17% годовых, тогда как VA 12.39%. Разница более процента! При этом на более волатильных рынках развивающихся стран (в том числе на российском рынке) стратегия должна показать как минимум не худший результат.

Недостатки усреднения стоимости

Усреднение стоимости спорный вариант при внесении большой суммы: расчеты показывают, что при наличии значительных средств и долгосрочной стратегии лучшим решением будет войти в рынок сразу. Даже упавшие акции и облигации принесут дивидендный и купонный доход, если вы в рынке. Вернувшись к первому примеру, мы получили 7% прибыли на внесенные средства, но не внесли 400$, которые остались «безработными».

Кроме того, у вас есть шанс упустить более высокую прибыль, если активы продолжат расти после первого инвестиционного периода. Иногда сильный бычий тренд может затянуться на годы, как в случае рынка США в период 1995-2000 годов. И DCA, и VA наиболее подходят либо для бокового рынка, либо для роста с сильными колебаниями. Но усреднение стоимости не сможет превратить плохой год в хороший.

Среднее арифметическое

Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее.

Среднее — очень информативная мера «центрального положения» наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.

Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится «истинное» (неизвестное) среднее популяции.

Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции.

Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он «накрывает» неизвестное среднее популяции, и наоборот.

Хорошо известно, например, что чем «неопределенней» прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.

Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок.

При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.

Довольно трудно «ощутить» числовые измерения, пока данные не будут содержательно обобщены. Диаграмма часто полезна в качестве отправной точки. Мы можем также сжать информацию, используя важные характеристики данных. В частности, если бы мы знали, из чего состоит представленная величина, или если бы мы знали, насколько широко рассеяны наблюдения, то мы бы смогли сформировать образ этих данных.

Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе.

Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной X можно изобразить как X₁, X₂, X₃, …, X_n. Например, за X можно обозначить рост индивидуума (см), X₁ обозначит рост 1-го индивидуума, а X_i — рост i-го индивидуума. Формула для определения среднего арифметического наблюдений (произносится «икс с чертой»):

= (Х₁ + Х₂ + … + X_n) / n

Можно сократить это выражение:

где (греческая буква «сигма») означает «суммирование», а индексы внизу и вверху этой буквы означают, что суммирование производится от i = 1 до i = n. Это выражение часто сокращают еще больше:

или

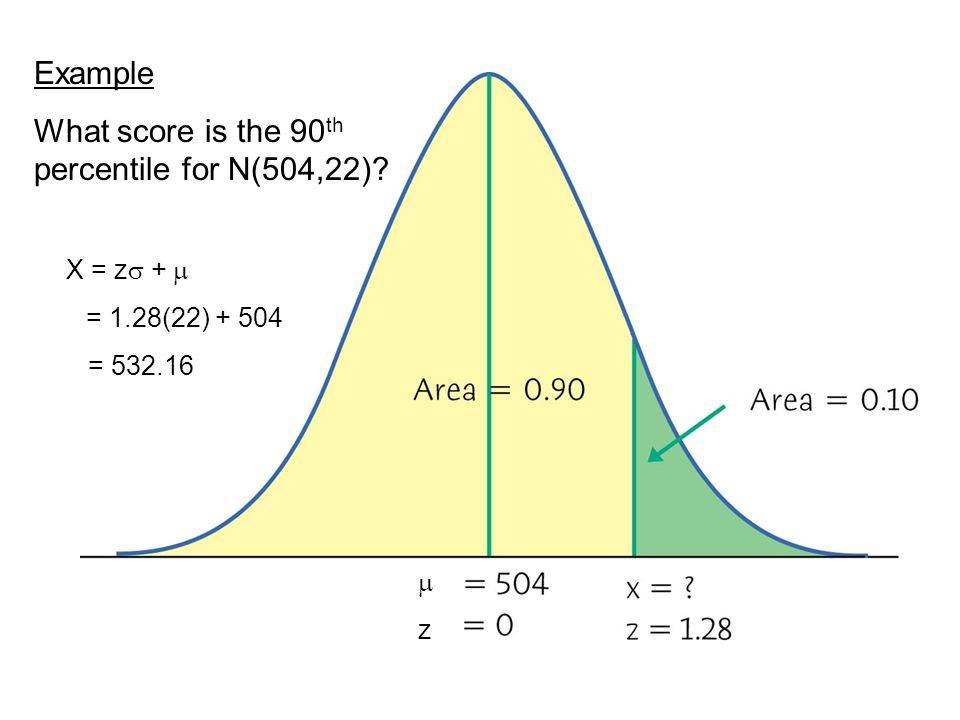
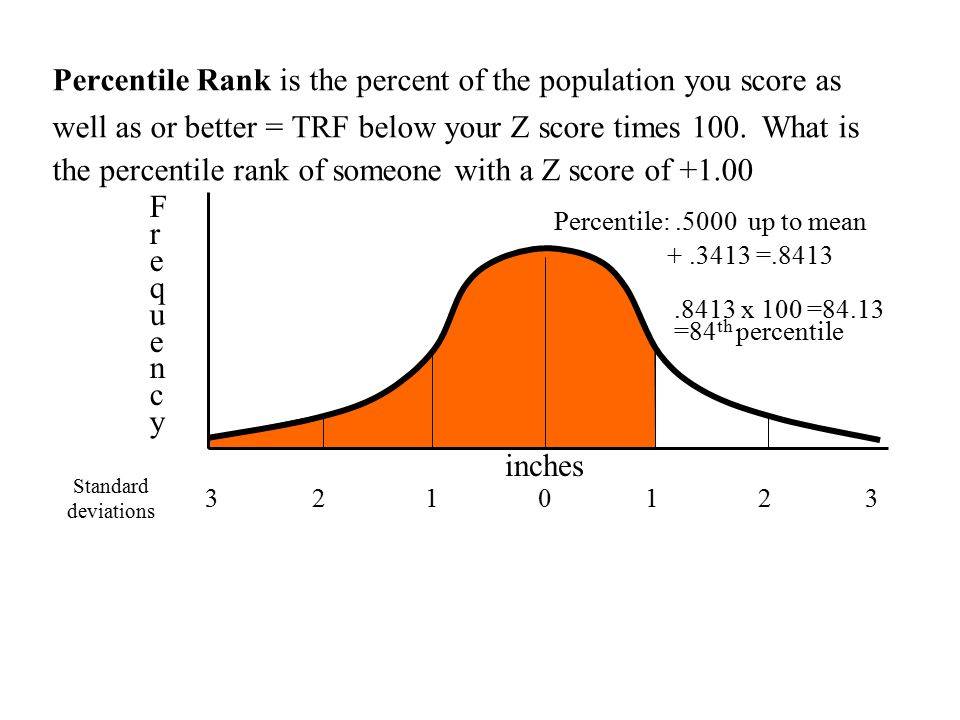
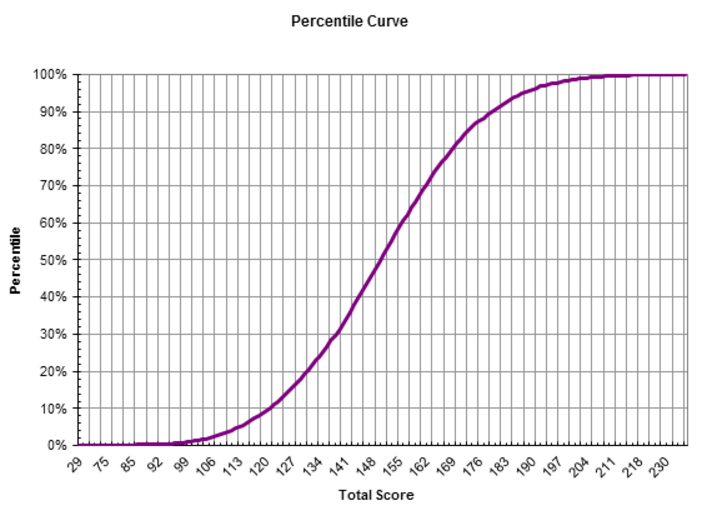
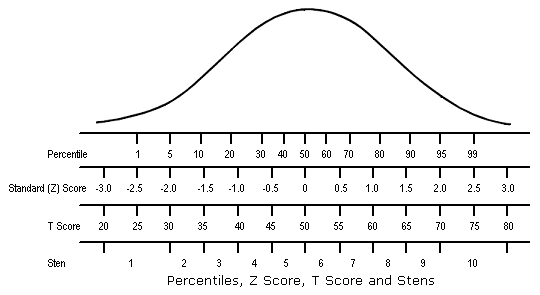
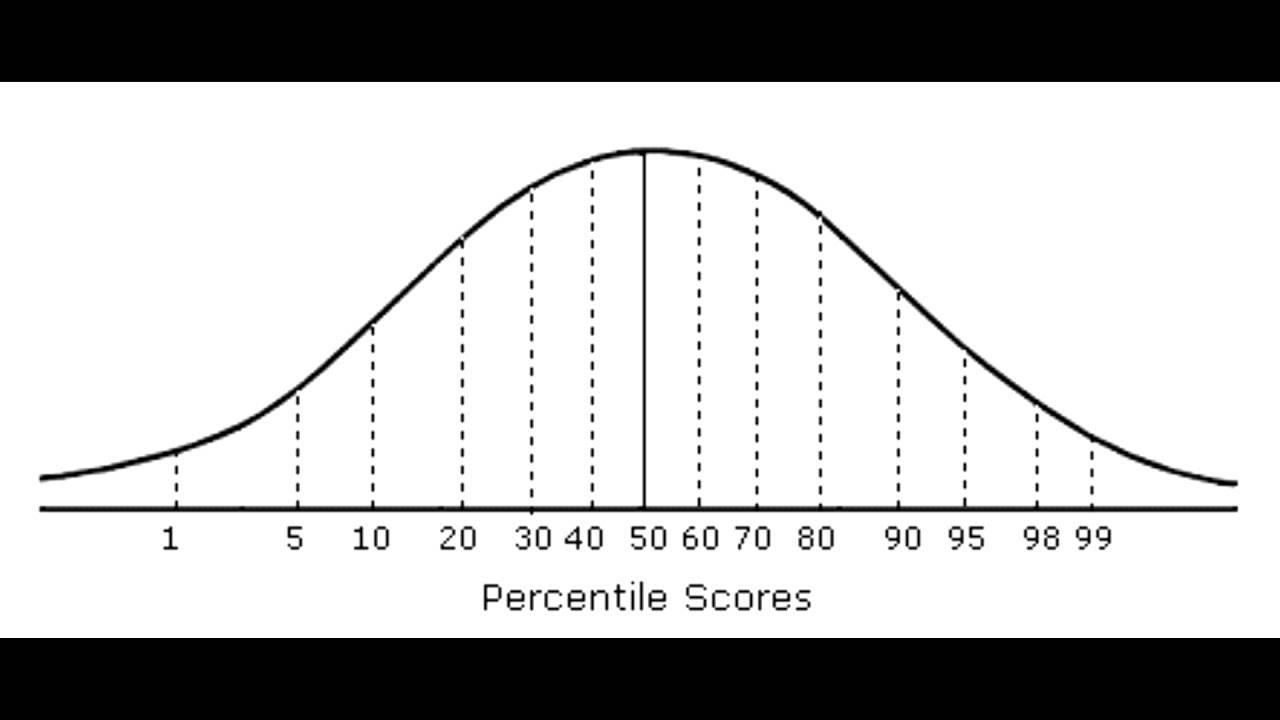
Нормальное распределение и процентили

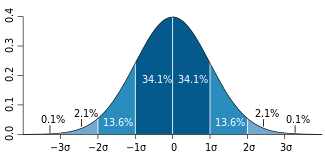
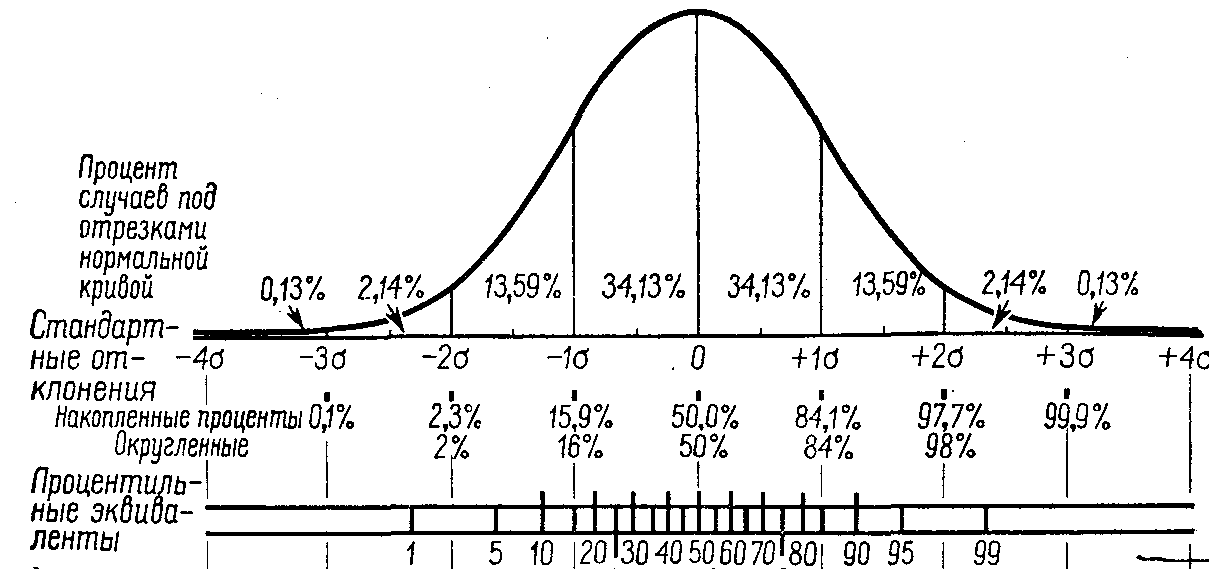
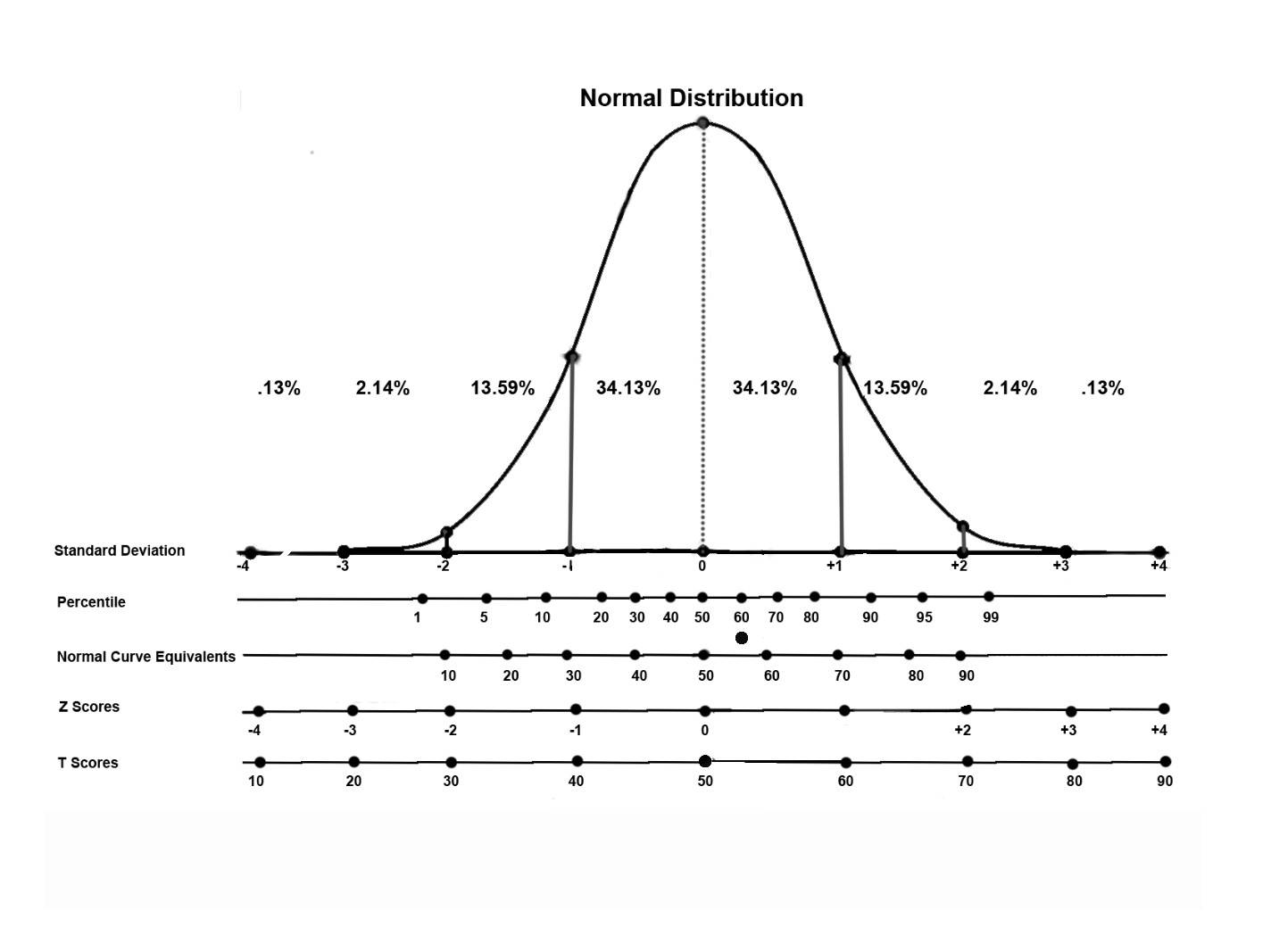
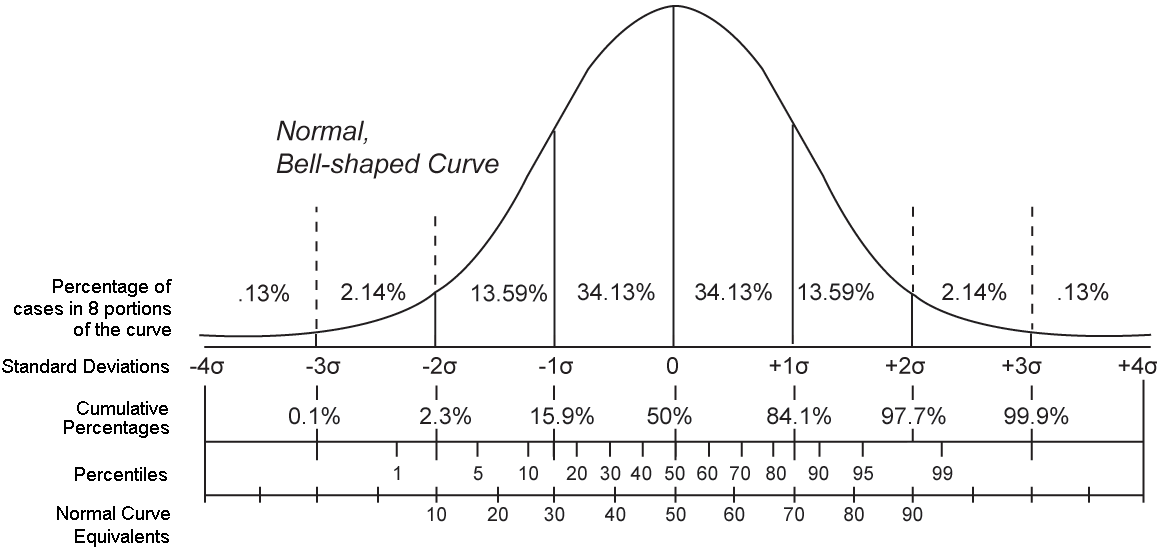
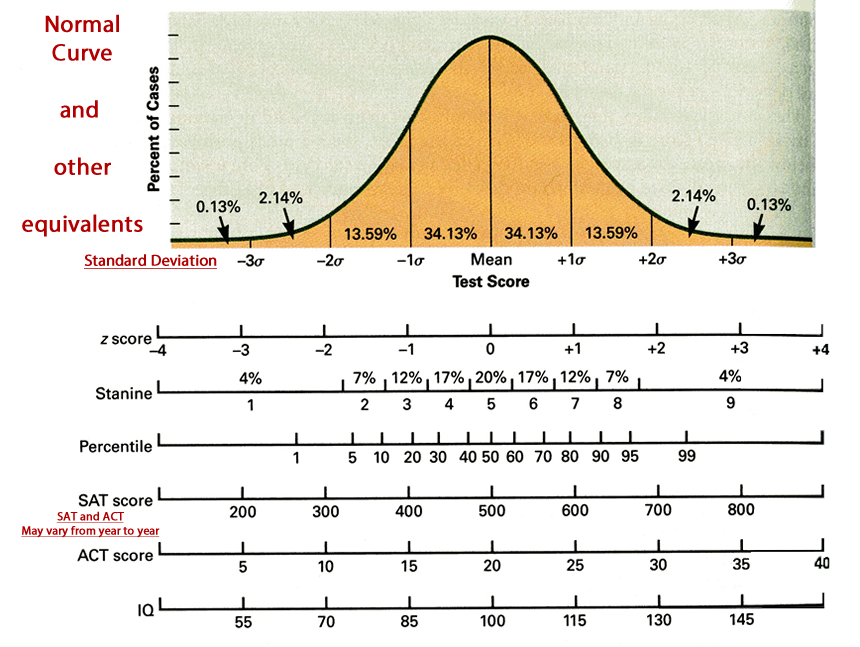
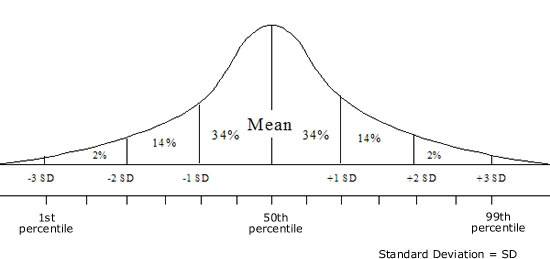
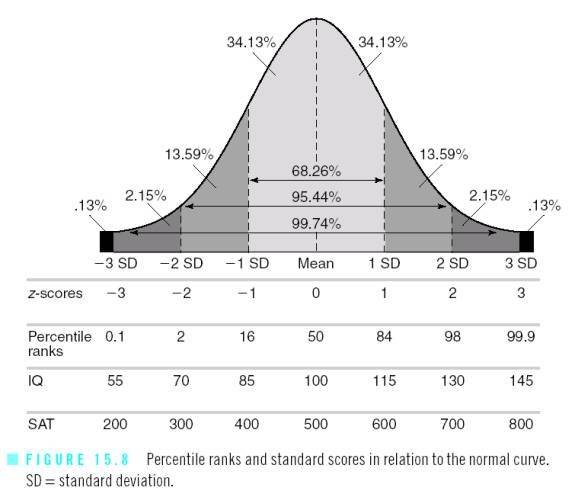
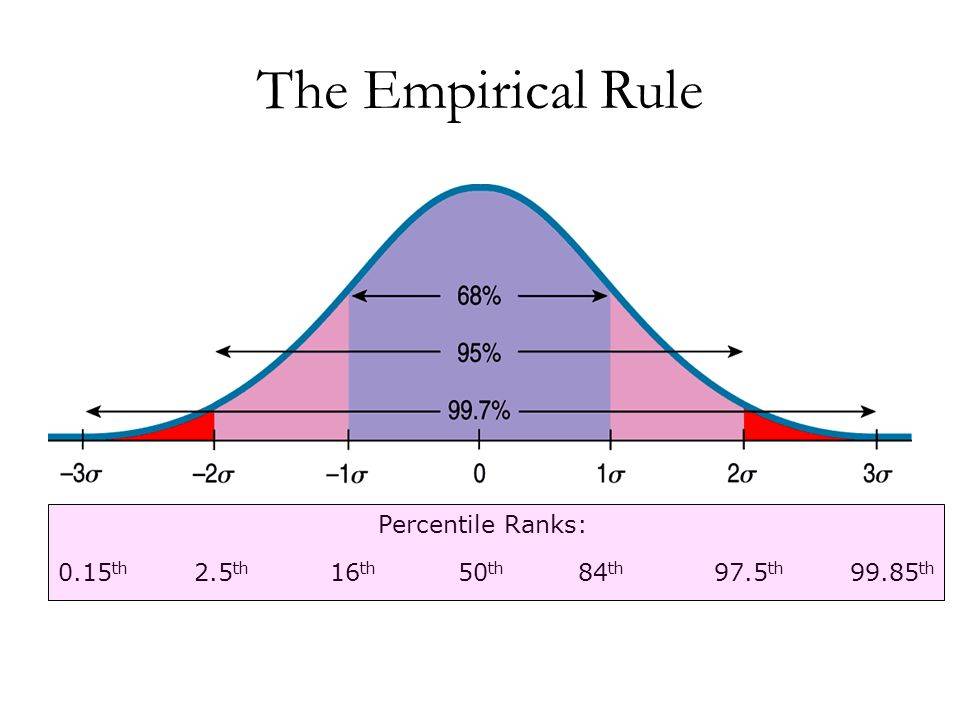
Представление правила трех сигм . Темно-синяя зона представляет наблюдения в пределах одного стандартного отклонения (σ) по обе стороны от среднего (μ), что составляет около 68,3% населения. Два стандартных отклонения от среднего значения (темно-синий и средний синий) составляют около 95,4%, а три стандартных отклонения (темный, средний и голубой) — около 99,7%.

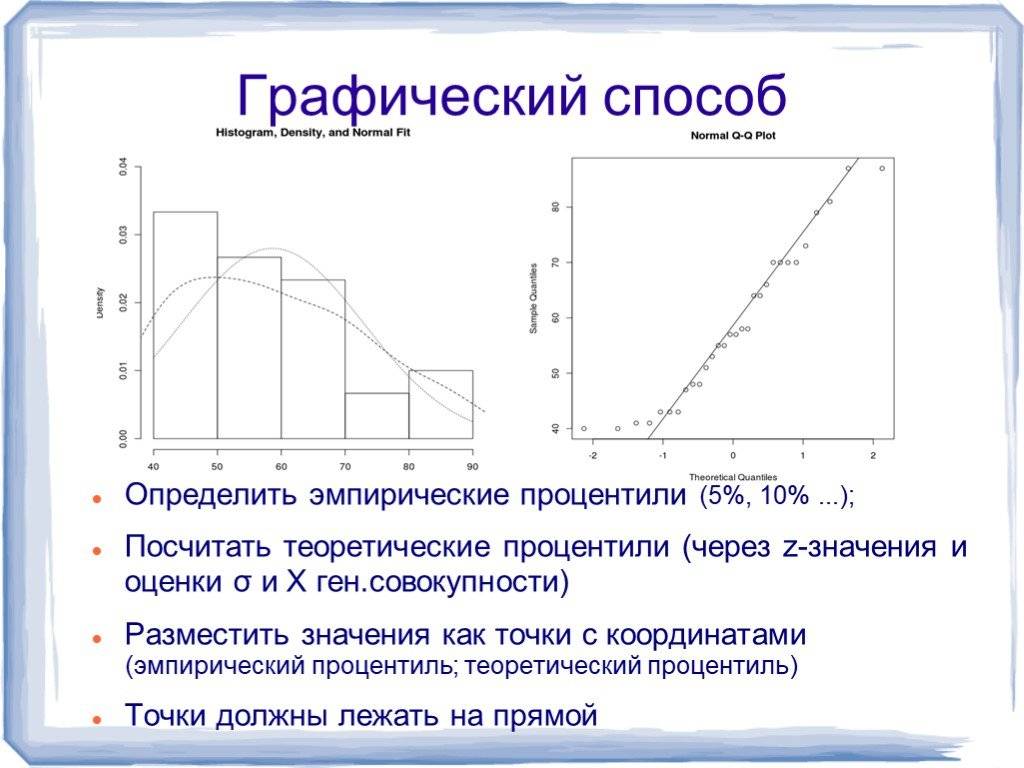
Методы, приведенные в разделе определений (ниже), являются приблизительными для использования в статистике малых выборок. В общих чертах, для очень больших популяций, следующих нормальному распределению , процентили часто могут быть представлены ссылкой на график нормальной кривой. Нормальное распределение откладывается по оси с точностью до стандартных отклонений или единиц сигмы ( ). Математически нормальное распределение простирается до отрицательной бесконечности слева и положительной бесконечности справа

Обратите внимание, однако, что только очень небольшая часть людей в популяции выйдет за пределы диапазона от –3 до +3. Например, с человеческим ростом очень мало людей выше +3 уровня роста.
σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}

Процентили представляют собой площадь под нормальной кривой, увеличивающуюся слева направо. Каждое стандартное отклонение представляет собой фиксированный процентиль. Таким образом, округляя до двух десятичных знаков, −3 — это 0,13-й процентиль, −2 — 2,28-й процентиль, -1 — 15,87-й процентиль, 0 — 50-й процентиль (как среднее, так и медианное значение распределения), +1 84,13-й процентиль. процентиль, +2 для 97,72-го процентиля и +3 для 99,87-го процентиля. Это связано с правилом 68–95–99,7 или правилом трех сигм

Обратите внимание, что теоретически 0-й процентиль попадает в отрицательную бесконечность, а 100-й процентиль — на положительную бесконечность, хотя во многих практических приложениях, таких как результаты тестов, применяются естественные нижние и / или верхние пределы.
σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}

Вариация в пределах субъектов и между субъектами

Если провести повторные измерения непрерывной переменной у исследуемого объекта, то можно увидеть ее изменения (внутрисубъектные изменения). Это можно объяснить тем, что объект не всегда может дать точные и те же самые ответы, и/или ошибкой, погрешностью измерения. Однако при измерениях у одного объекта вариация обычно меньше, чем вариация единичного измерения в группе (межсубъектные изменения).

Например, вместимость легкого 17-летнего мальчика составляет от 3,60 до 3,87 л, когда измерения повторяются не менее 10 раз; если провести однократное измерение у 10 мальчиков того же возраста, то объем будет между 2,98 и 4,33 л. Эти концепции важны в плане исследования.

Связанные определения:Выборочное среднее, среднее значение выборкиВыбросДисперсия (рассеяние, разброс)Дисперсия выборки (выборочная дисперсия)Коэффициент вариацииМаксимумМатематическое ожидание дискретной случайной величиныМатематическое ожидание непрерывной случайной величиныМедианаМеры дисперсии, меры разбросаМинимумМодаОписательные статистикиОписательный анализПараметры рассеянияПараметры центральной тенденцииСреднее значениеСреднеквадратичное отклонение популяцииСтандартная ошибка среднегоСтандартное отклонение

Разница между процентами и процентилем

Определение: Процент — это число из 100, а процентили — нет.
Позиция: Percentile — это значение, ниже которого определен определенный процент значений.
Условное обозначение: Символ процента — знак процента,%, а процентиль обозначен х-м, где x — число, так, например, 25го
Квартили: Процентники имеют квартили, а проценты — нет.
Ранг: Percentiles основаны на ранжированных числах, а проценты — нет.
Десятичные: Проценты могут быть записаны как десятичные числа, процентили не могут быть записаны как десятичные.
соотношение: Проценты могут быть записаны как отношение, в то время как процентили не могут быть записаны как отношение.
Основано на: Процент основан на одном случае, а процентиль основан на сравнении одного случая со всеми случаями в конкретной ситуации.
распределение: Percentiles полагаются на нормальное распределение, а проценты — нет.

Коромысло

Ловля с коромыслом приобрела популярность у наших рыболовов много лет назад. И по сей день большинство использует именно коромысло. Во многих регионах страны название «коромысло» ассоциируется со снастью для ловли щуки и окуня. Многие изготавливают самостоятельно из аналогичных приспособлений, популярных у доночников, прикрепляя к одному «плечу» грузило, а к другому поводок с приманкой.

Интересной конструкция становится в том случае, если в качестве элементов огрузки использовать съемные дробинки весом 3-4 г. В этом случае, не меняя оснастки, рыболов может за несколько минут подобрать груз необходимого веса для конкретных условий.