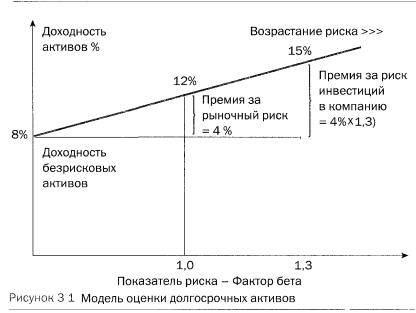
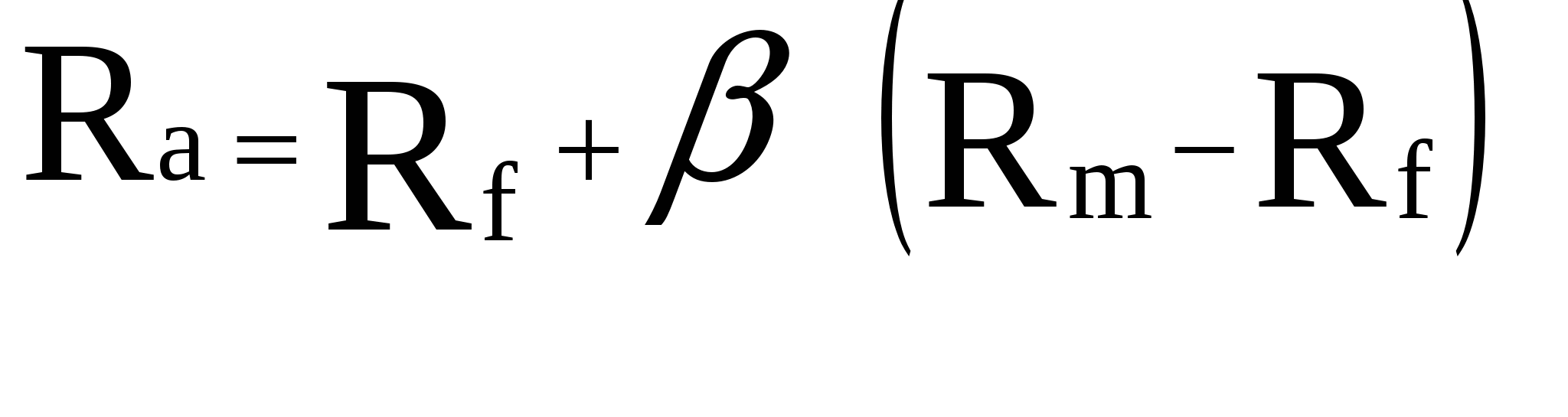Модель ценообразования основных средств — capital asset pricing model

Требуемый доход от актива

CAPM возвращает соответствующую активу требуемую доходность или ставку дисконтирования, т. Е. Ставку, по которой будущие денежные потоки, создаваемые активом, должны дисконтироваться с учетом относительной рискованности этого актива.

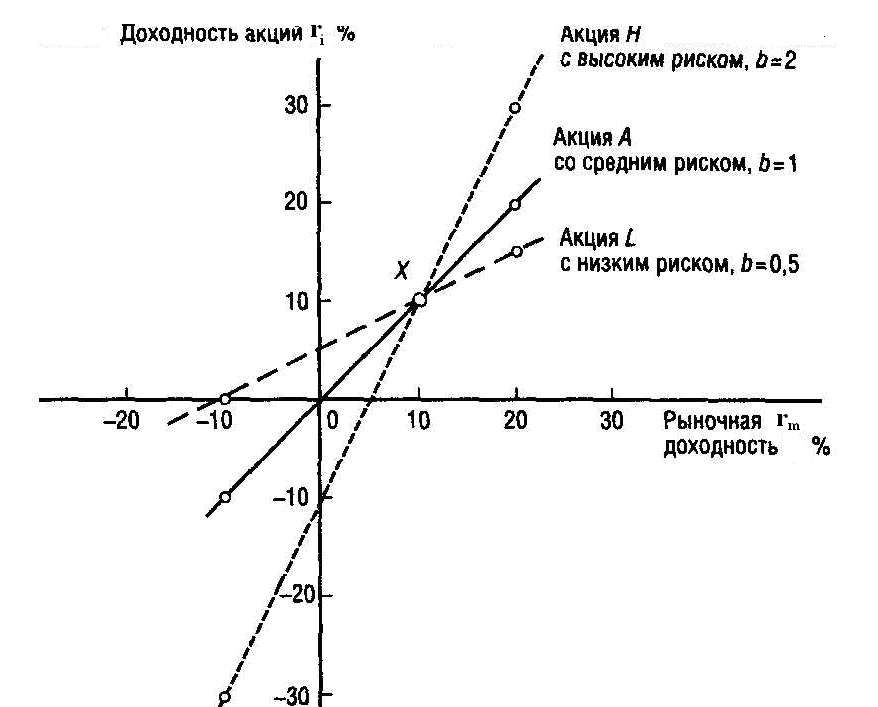
Бета, превышающая единицу, означает более чем средний уровень «рискованности»; бета-версии ниже единицы указывают ниже среднего. Таким образом, более рискованная акция будет иметь более высокий бета-коэффициент и будет дисконтироваться по более высокой ставке; менее чувствительные акции будут иметь более низкие бета-ставки и будут дисконтированы по более низкой ставке. Учитывая принятую вогнутую функцию полезности , CAPM согласуется с интуицией — инвесторы (должны) требовать более высокой прибыли за владение более рискованным активом.

Поскольку бета отражает чувствительность активов к недиверсифицируемым, то есть рыночным рискам , рынок в целом по определению имеет бета, равную единице. Индексы фондовых рынков часто используются в качестве локальных индикаторов рынка — и в этом случае (по определению) имеют бета, равную единице. Таким образом, инвестор в большой диверсифицированный портфель (такой как паевой инвестиционный фонд ) ожидает, что его результаты будут соответствовать рыночным.

Изобретатели

CAPM была введена Джеком Трейнором (1961, 1962), Уильямом Ф. Шарпом (1964), Джоном Линтнером (1965a, b) и Яном Моссином (1966) независимо друг от друга, основываясь на более ранней работе Гарри Марковица по диверсификации и современной теории портфеля. . Шарп, Марковиц и Мертон Миллер совместно получили Нобелевскую премию по экономике 1990 года за свой вклад в область финансовой экономики . Фишер Блэк (1972) разработал другую версию CAPM, названную Black CAPM или нулевой бета-версией CAPM, которая не предполагает существования безрискового актива. Эта версия была более устойчивой к эмпирическим проверкам и повлияла на широкое распространение CAPM.

В заключении …

Сбербанк по праву считается одним из наиболее проверенных, стабильных и надёжных банков Российской Федерации. Естественно, общее количество нарушений нормативных актов, а уж тем более, законодательных, здесь – большая редкость. Даже в сравнении с банками, имеющими коммерческую основу. Тем не менее, клиенты банка имеют полное право отстаивать свои гражданские права и писать жалобы в том случае, если с подобными нарушениями столкнутся.

Куда обращаться?

Если вас не устраивают какие-то аспекты обслуживания, то вы должны в первую очередь обратиться за разъяснениями в ближайшие отделения Сбербанка.

При обращении в Сбербанк необходимо воспользоваться одним из предложенных вариантов для связи. С их помощью можно задать вопрос, указав все свои контакты.

Обращение можно подать и через Центробанк, а также прочие инстанции. Однако отправление заявления напрямую в Сбербанк имеет ряд преимуществ:

Ответ будет подготовлен быстрее
Принципы принятия решений не меняются в зависимости от канала обращения: даже при подаче заявления через ЦБ все равно будут применяться те же единые установленные процедуры, как и при обращении напрямую в финансовую организацию
На официальном портале банка есть возможность отслеживать статус жалобы (этого нет при обращении в иные внешние каналы)
Обращение напрямую позволяет запросить какие-либо необходимые документы через личный кабинет (Сбербанк Онлайн), что освобождает от походов с бумажными носителями в ВСП или иные организации
При несогласии с ответом от ЦЗК банка, можно оспорить это решение в службе омбудсмена, подчиняющейся напрямую президенту финансовой организации. Ее специалисты перепроверят законность предыдущего решения ЦЗК

Стоимость активов

После того, как ожидаемая / требуемая норма доходности рассчитана с использованием CAPM, мы можем сравнить эту требуемую норму доходности с предполагаемой доходностью актива в течение определенного инвестиционного горизонта, чтобы определить, будет ли это подходящим вложением. Для этого сравнения вам потребуется независимая оценка перспектив доходности ценной бумаги, основанная на фундаментальных или технических методах анализа , включая P / E, M / B и т. Д.
E(ря){\ displaystyle E (R_ {i})}

Предполагая, что CAPM верен, актив правильно оценивается, когда его расчетная цена совпадает с приведенной стоимостью будущих денежных потоков от актива, дисконтированных по ставке, предложенной CAPM. Если оценочная цена выше, чем оценка CAPM, то актив недооценен (и переоценен, когда оценочная цена ниже оценки CAPM). Если актив не находится на SML, это также может указывать на неправильную оценку. Поскольку ожидаемая доходность актива во время равна , более высокая ожидаемая доходность, чем то, что предлагает CAPM, указывает на то, что она слишком низкая (актив в настоящее время недооценен), предполагая, что в момент времени актив вернется к предложенной цене CAPM.
т{\ displaystyle t}E(рт)знак равноE(пт+1)-птпт{\ Displaystyle E (R_ {t}) = {\ frac {E (P_ {t + 1}) — P_ {t}} {P_ {t}}}}пт{\ displaystyle P_ {t}}т+1{\ displaystyle t + 1}

Цена актива с использованием CAPM, иногда называемая формулой ценообразования, эквивалентной достоверности, представляет собой линейную зависимость, определяемую формулой
п{\ displaystyle P_ {0}}

пзнак равно11+ржE(пТ)-Cоv(пТ,рM)(E(рM)-рж)Vар(рM){\ displaystyle P_ {0} = {\ frac {1} {1 + R_ {f}}} \ left }

где — доходность актива или портфеля.
пТ{\ Displaystyle P_ {T}}

Формула

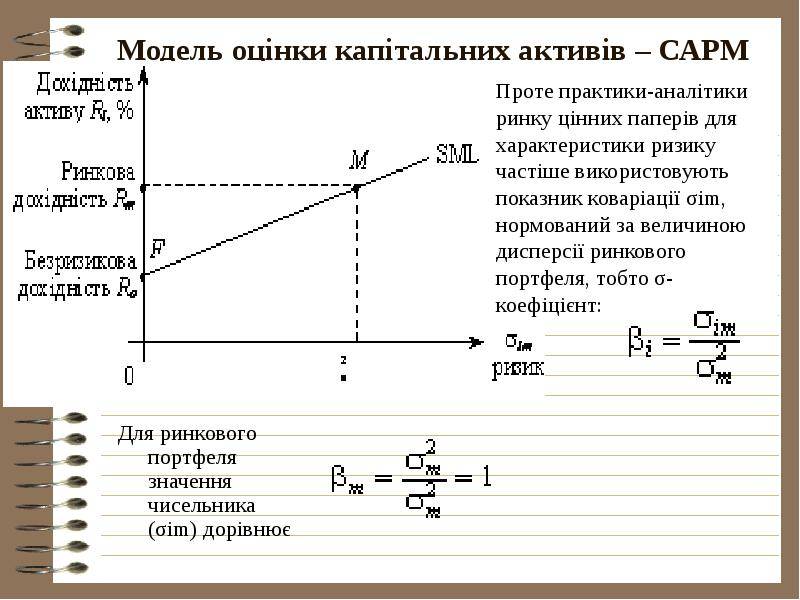
CAPM — это модель ценообразования для отдельной ценной бумаги или портфеля. Для отдельных ценных бумаг мы используем линию рынка ценных бумаг (SML) и ее отношение к ожидаемой доходности и систематическому риску (бета), чтобы показать, как рынок должен оценивать отдельные ценные бумаги в соответствии с их классом риска безопасности. SML позволяет нам рассчитать отношение прибыли к риску для любой ценной бумаги по отношению к рынку в целом. Следовательно, когда ожидаемая норма прибыли для любой ценной бумаги дефлируется на ее бета-коэффициент, отношение вознаграждения к риску для любой отдельной ценной бумаги на рынке равно отношению рыночной прибыли к риску, таким образом:

E(ря)-ржβязнак равноE(рм)-рж{\ displaystyle {\ frac {E (R_ {i}) — R_ {f}} {\ beta _ {i}}} = E (R_ {m}) — R_ {f}})

Отношение рыночного вознаграждения к риску фактически представляет собой премию за рыночный риск, и, перестроив приведенное выше уравнение и решив его , мы получаем модель ценообразования капитальных активов (CAPM).
E(ря){\ displaystyle E (R_ {i})}

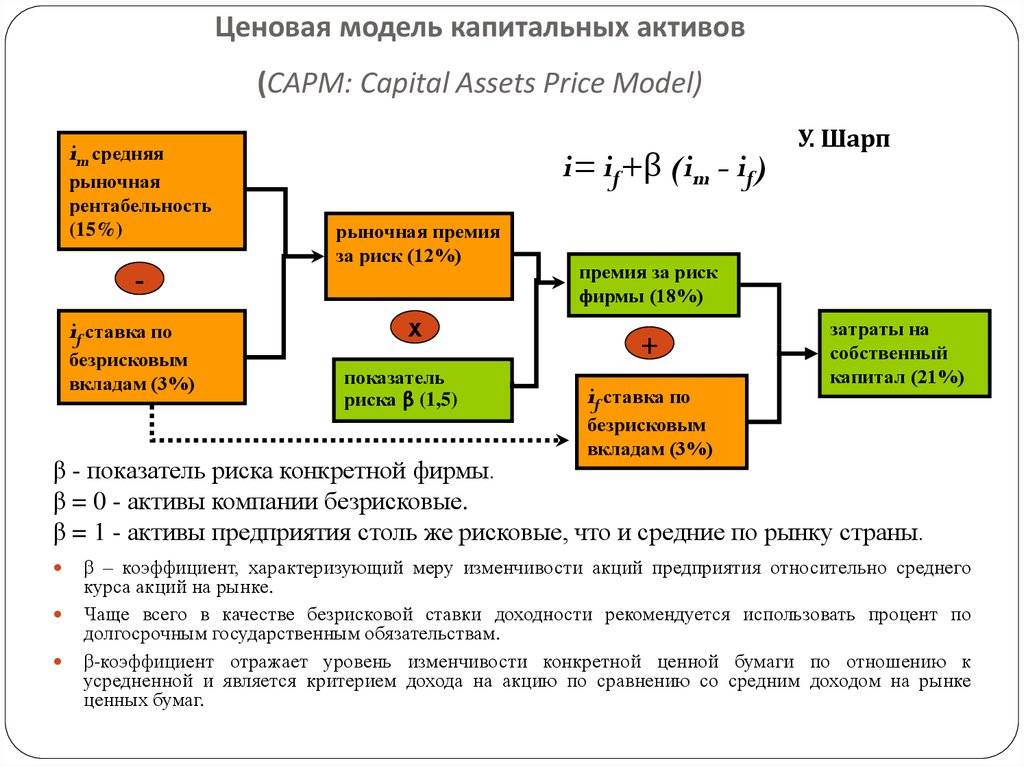
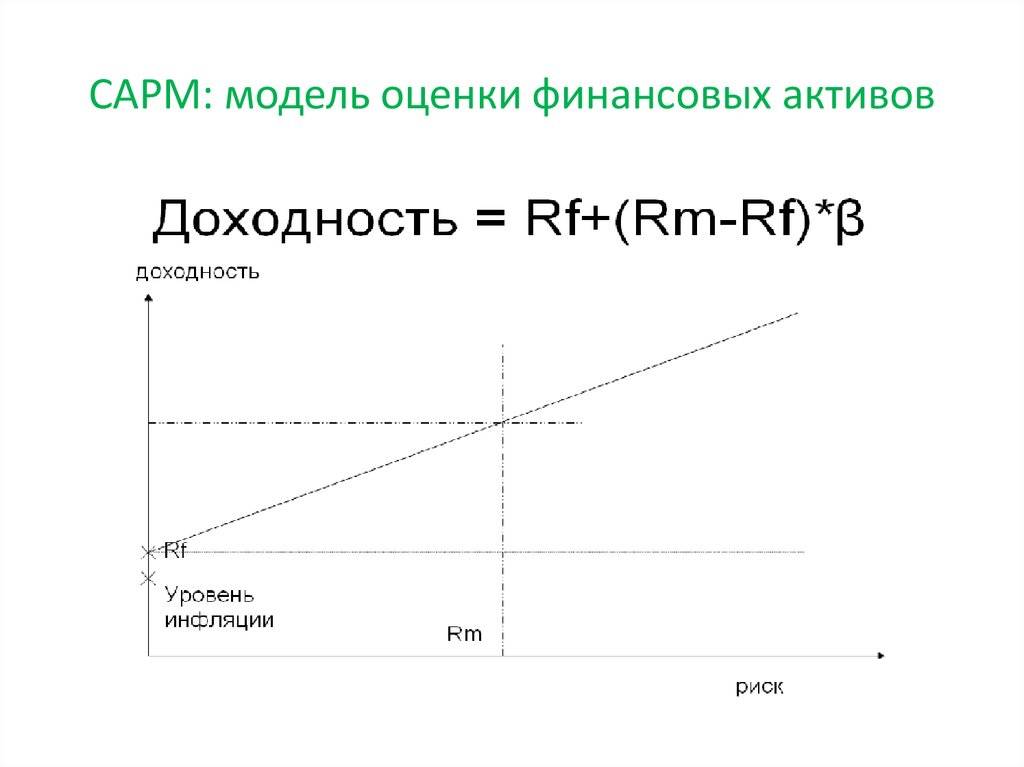
E(ря)знак равнорж+βя(E(рм)-рж){\ Displaystyle E (R_ {i}) = R_ {f} + \ beta _ {i} (E (R_ {m}) — R_ {f}) \,}

где:

E(ря) {\ displaystyle E (R_ {i}) ~~} ожидаемая доходность основного капитала
рж {\ displaystyle R_ {f} ~} это безрисковая процентная ставка, такая как проценты по государственным облигациям
βя {\ displaystyle \ beta _ {я} ~~}( бета ) — это чувствительность ожидаемой избыточной доходности активов к ожидаемой избыточной рыночной доходности, или такжеβязнак равноCоv(ря,рм)Vар(рм)знак равноρя,мσяσм{\ displaystyle \ beta _ {i} = {\ frac {\ mathrm {Cov} (R_ {i}, R_ {m})} {\ mathrm {Var} (R_ {m})}} = \ rho _ { я, м} {\ frac {\ sigma _ {i}} {\ sigma _ {m}}}}
E(рм) {\ displaystyle E (R_ {m}) ~} ожидаемая доходность рынка
E(рм)-рж {\ displaystyle E (R_ {m}) — R_ {f} ~}иногда называют рыночной премией (разница между ожидаемой рыночной нормой доходности и безрисковой нормой доходности).
E(ря)-рж {\ displaystyle E (R_ {i}) — R_ {f} ~}также известна как премия за риск
ρя,м{\ displaystyle \ rho _ {я, м}}обозначает коэффициент корреляции между инвестицией и рынкомя{\ displaystyle i}м{\ displaystyle m}
σя{\ displaystyle \ sigma _ {я}}это стандартное отклонение для инвестицийя{\ displaystyle i}
σм{\ displaystyle \ sigma _ {m}}это стандартное отклонение для рынка .м{\ displaystyle m}

В пересчете на премию за риск мы находим, что:

E(ря)-ржзнак равноβя(E(рм)-рж){\ Displaystyle E (R_ {i}) — R_ {f} = \ beta _ {i} (E (R_ {m}) — R_ {f}) \,}

в котором говорится, что индивидуальная премия за риск равна рыночной премии, умноженной на β .

Примечание 1: ожидаемая рыночная ставка доходности обычно оценивается путем измерения среднего арифметического исторических доходностей рыночного портфеля (например, S&P 500).

Примечание 2: безрисковая норма доходности, используемая для определения премии за риск, обычно представляет собой среднее арифметическое исторических безрисковых норм доходности, а не текущую безрисковую норму доходности.

Полный вывод см. В современной теории портфеля .

Способы

Места для ловли каждый рыболов выбирает по своему вкусу. Одни предпочитают удить с берега, другие — с лодки. Однако нужно учитывать, что для использования плавсредств требуется получить разрешение, в противном случае сотрудники госинспекции, занимающиеся маломерными судами, могут выписать штраф. Берега Оки в районе Муромского региона преимущественно травянистые и заросшие. Поэтому здесь достаточно интересно ловить хищников, например, на щуку.

Самая распространенная рыбалка в Муроме на Оке проходит с использованием троллинга. Судя по отзывам, ловля на дорожку очень эффективна во время ужения с лодки. Не меньшей популярностью здесь пользуется и джиговая ловля. Это достаточно увлекательное и интересное занятие. При этом главное – правильно подобрать снасти.

Эффективная граница

Граница эффективности (Марковица) . CAL означает линию распределения капитала .

CAPM предполагает, что профиль риска и доходности портфеля может быть оптимизирован — оптимальный портфель отображает минимально возможный уровень риска для своего уровня доходности. Кроме того, поскольку каждый дополнительный актив, вводимый в портфель, дополнительно диверсифицирует портфель, оптимальный портфель должен включать каждый актив (при условии отсутствия торговых затрат), причем каждый актив должен быть взвешен по стоимости для достижения вышеуказанного (при условии, что любой актив является бесконечно делимым ). Все такие оптимальные портфели, то есть по одному для каждого уровня доходности, составляют эффективную границу.

Поскольку несистематический риск поддается диверсификации , общий риск портфеля можно рассматривать как бета- коэффициент .

Когда платить налог не нужно

Доходы не облагаются налогом, если это:
️ Алименты
️ Благотворительная помощь
️ Пособия и стипендии
️ Суточные в рамках лимита
️ Возмещение судебных расходов
️ Деньги и имущество, доставшиеся по наследству
️ Доходы от продажи овощей и фруктов с огорода и т.д.

Полный список гораздо длиннее, свериться можно здесь. В какой форме вы получили эти деньги (наличными, на карту и т.д.), не имеет значения.

Бывает, что вы вернули коллеге долг. Или все сбросились вам на карту, чтобы купить общий подарок. Или кто-то заболел, и друзья решили помочь. Или бабушка пополнила карту внука, чтобы он мог купить новый гаджет.

Всё это – не доход. А значит, налоги с таких переводов платить не нужно.

Подарки от физлиц тоже не облагаются налогом. Исключение – только если не близкие родственники дарят машину, недвижимость или акции на сумму от 4 тыс. рублей. У них лучше брать деньгами 🙂

Если компания или ИП сделали вам подарок дешевле 4 тыс. рублей, вы можете не платить с него налог. А если это презент к рождению ребенка, то налог можно не платить, если цена подарка меньше 50 тыс.

Требуемый доход от актива

Общий вид модели арбитражного ценообразования.

Теория
арбитражного ценообразования (АРТ) была
предложена профессором Йельского
университета С. Россом в 1976 г. и является
альтернативной САРМ моделью общего равновесия
на финансовом рынке. Главным предположением
теории является то, что каждый инвестор
стремится использовать возможность увеличения
доходности своего портфеля без увеличения
риска. Механизмом, способствующим реализации
данной возможности, является арбитражный
портфель.10Арбитраж
(arbitrage) — это получение безрисковой
прибыли путем использования
разных цен на одинаковую продукцию
или ценные бумаги. Арбитраж, являющийся
широко распространенной инвестиционной
тактикой, обычно состоит из продажи
ценной бумаги по относительно высокой
цене и одновременной покупки
такой же ценной бумаги (или ее функционального
эквивалента) по относительно низкой цене

Арбитражная деятельность является
важной составляющей современных эффективных
рынков ценных бумаг. Поскольку арбитражные
доходы являются безрисковыми по определению,
то все инвесторы стремятся получать
такие доходы при каждой возможности

Определить,
подходит ли ценная бумага или портфель
для арбитражных операций, можно
различными способами. Одним из них
является анализ общих факторов, которые
влияют на курс ценных бумаг. Факторная
модель подразумевает, что ценные бумаги
или портфели с одинаковыми чувствительностями
к факторам ведут себя одинаково,
за исключением внефакторного риска.
Поэтому ценные бумаги или портфели
с одинаковыми чувствительностями
к факторам должны иметь одинаковые
ожидаемые доходности, в противном
случае имелись бы «почти арбитражные»
возможности. Но как только такие возможности
появляются, деятельность инвесторов
приводит к их исчезновению.Таким
образом, в основе модели арбитражного
ценообразования лежит утверждение
о том, что фактическая доходность
любой акции складывается из двух
частей: нормальной, или ожидаемой,
доходности и рисковой, или неопределенной
доходности. Последний компонент
определяется многими экономическими
факторами, например, рыночной ситуацией
в стране, инфляцией, динамикой процентных
ставок и др.В
наиболее общем виде модель арбитражного
ценообразования описывается следующей
зависимостью:

Риск и диверсификация

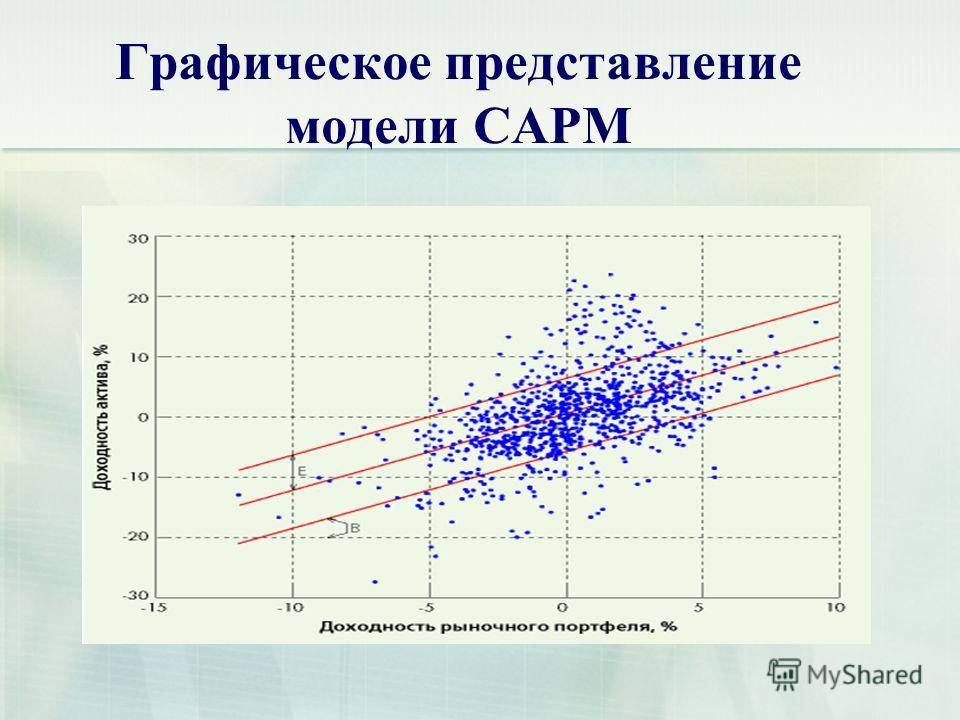
Риск портфеля включает систематический риск , также известный как недиверсифицируемый риск, и несистематический риск, который также известен как идиосинкратический риск или диверсифицируемый риск. Под систематическим риском понимается риск, общий для всех ценных бумаг, то есть рыночный риск . Несистематический риск — это риск, связанный с отдельными активами. Несистематический риск можно диверсифицировать до меньших уровней путем включения большего количества активов в портфель (конкретные риски «усредняются»). То же самое невозможно для систематического риска на одном рынке. В зависимости от рынка портфель из примерно 30–40 ценных бумаг на развитых рынках, таких как Великобритания или США, сделает портфель достаточно диверсифицированным, так что подверженность риску ограничивается только систематическим риском. На развивающихся рынках требуется большее количество из-за более высокой волатильности активов.

Рациональный инвестор не должен брать на себя какие-либо диверсифицируемые риски, поскольку в рамках этой модели вознаграждаются только недиверсифицируемые риски. Следовательно, требуемая доходность актива, то есть доход, который компенсирует принятый риск, должен быть связан с его рискованностью в контексте портфеля, то есть его вкладом в общую рискованность портфеля, в отличие от его «отдельного риска». В контексте CAPM риск портфеля представлен более высокой дисперсией, т.е. меньшей предсказуемостью. Другими словами, бета-коэффициент портфеля является определяющим фактором при вознаграждении за систематические риски инвестора.

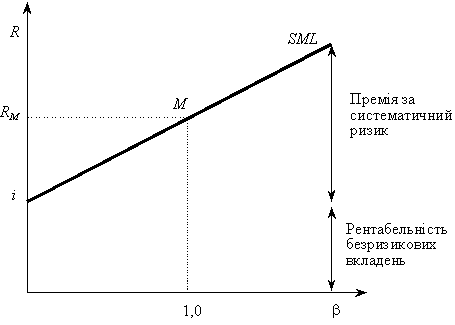
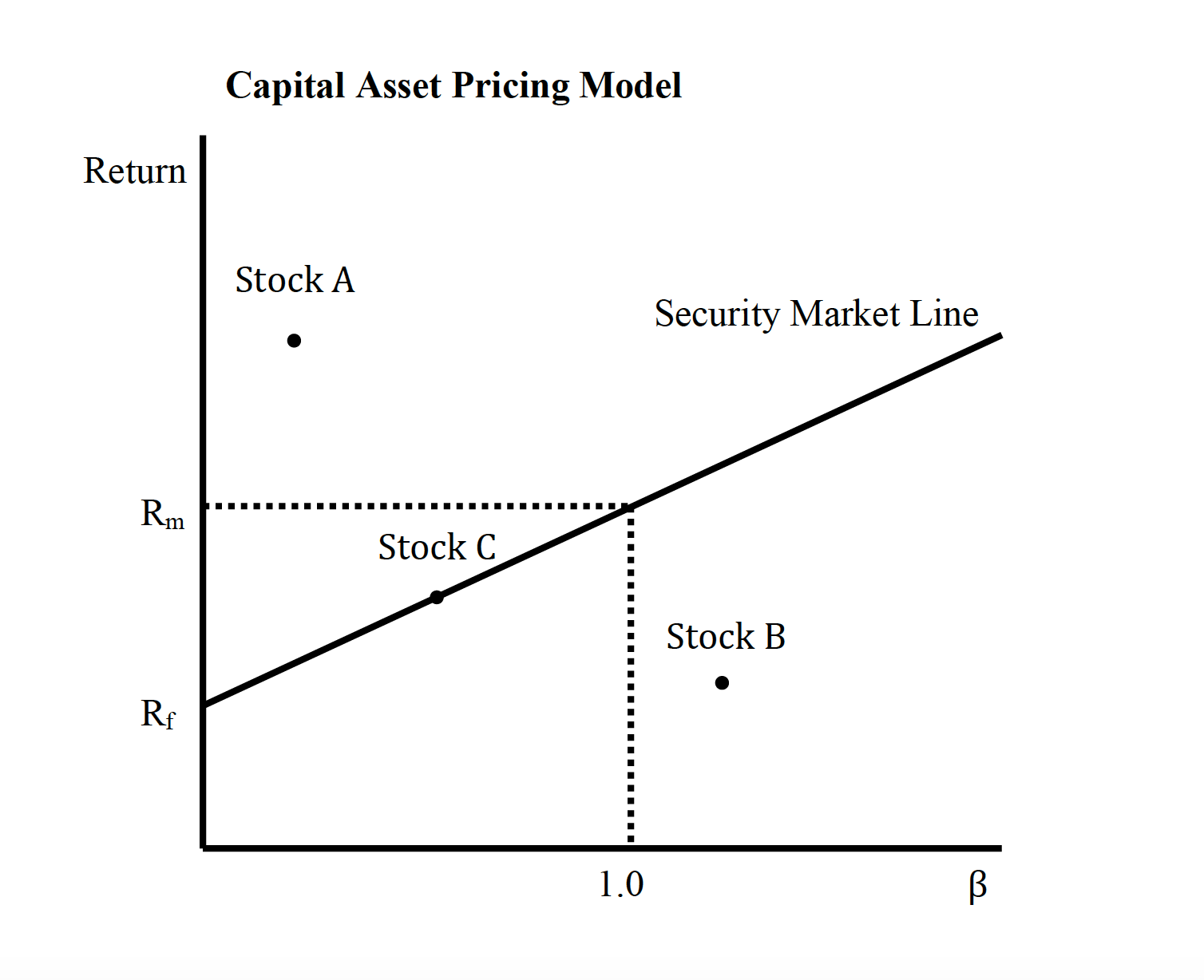
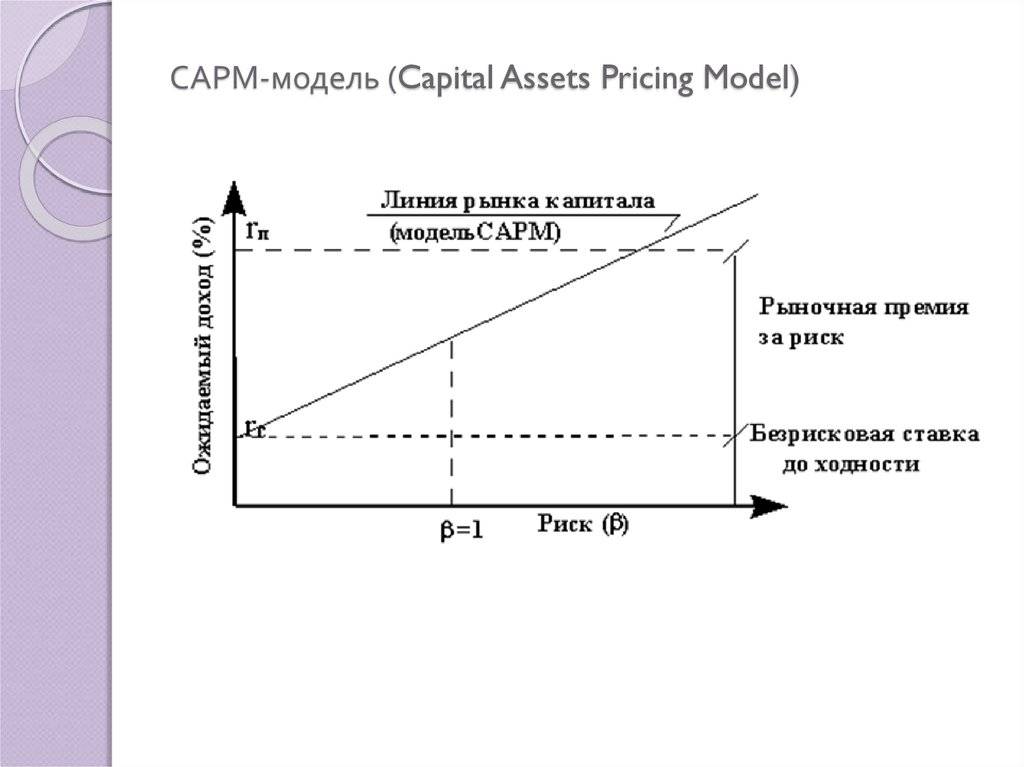
Линия рынка ценных бумаг

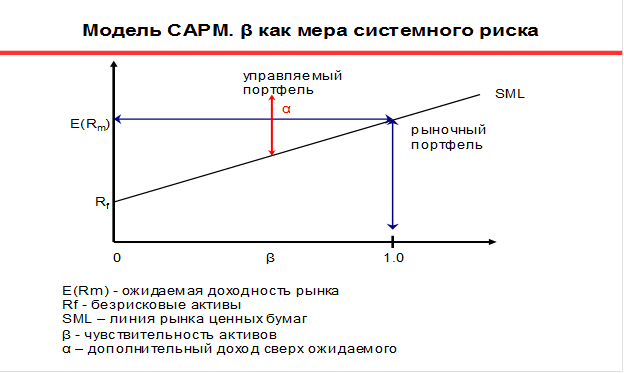
SML графы результаты от капитальных активов модель ценообразования (CAPM) формулы. Х Оу представляет риск (бета), а у оси х представляет собой ожидаемую доходность. Премия за рыночный риск определяется по наклону SML.

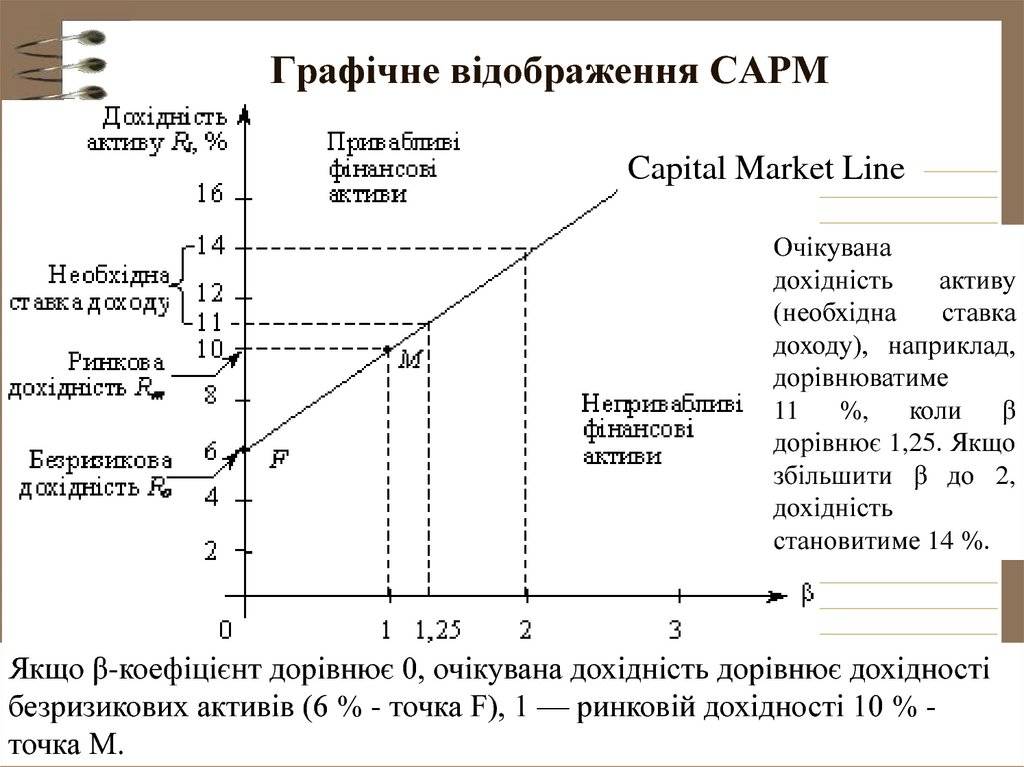
Связь между β и требуемой доходностью отображается на линии рынка ценных бумаг (SML), которая показывает ожидаемую доходность как функцию от β. Пересечение — это номинальная безрисковая ставка, доступная для рынка, а наклон — это рыночная премия E ( R _m ) — R _f . Линия рынка ценных бумаг может рассматриваться как представляющая однофакторную модель цены актива, где β — это подверженность изменениям стоимости рынка. Таким образом, уравнение SML выглядит следующим образом:

SMLE(ря)знак равнорж+βя(E(рM)-рж). {\ displaystyle \ mathrm {SML}: E (R_ {i}) = R_ {f} + \ beta _ {i} (E (R_ {M}) — R_ {f}). ~}

Это полезный инструмент для определения того, предлагает ли актив, рассматриваемый в портфеле, разумную ожидаемую доходность за свой риск. Отдельные ценные бумаги нанесены на график SML. Если ожидаемая доходность ценной бумаги в сравнении с риском нанесена на график выше SML, она недооценена, поскольку инвестор может рассчитывать на большую доходность за неотъемлемый риск. А ценная бумага, изображенная ниже SML, переоценена, поскольку инвестор согласился бы на меньшую прибыль на сумму принятого риска.

Акции и облигации: в чем разница и как торговать?

Май 12, 2018
Автор Марина Кириенко
Блог о трейдинге, Теория и практика
Комментарии к записи Акции и облигации: в чем разница и как торговать? отключены

Линия рынка ценных бумаг

SMLE(ря)знак равнорж+βя(E(рM)-рж). {\ displaystyle \ mathrm {SML}: E (R_ {i}) = R_ {f} + \ beta _ {i} (E (R_ {M}) — R_ {f}). ~}

Как заработать на инвестировании в акции

Инвестируя в фондовый рынок, вы можете заработать одним из двух способов:

Если цена акций возрастет, вы получите прирост капитала, если продадите акции по более высокой цене

Тем не менее, важно помнить, что, если цена акции упадет с вашей первоначальной цены покупки, вы потеряете деньги.
В некоторых случаях вы также можете получить часть прибыли компании в виде дивидендов, которые обычно выплачиваются два раза в год, но это зависит от конкретной компании. Имейте в виду, что не все компании платят дивиденды, а лишь те, которые видят в этом способ вознаграждения своих акционеров.