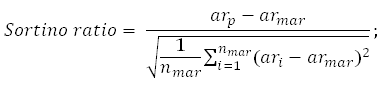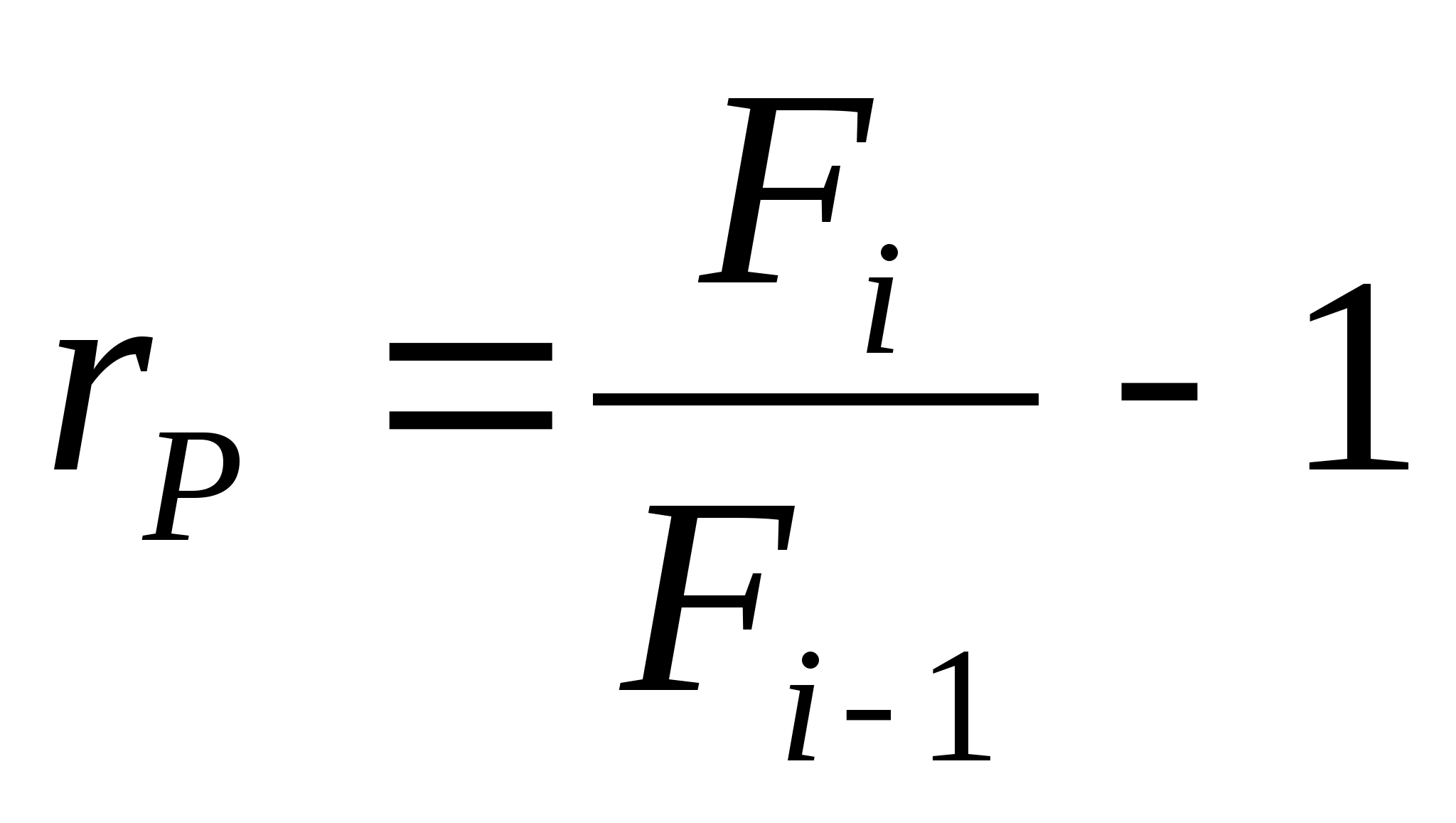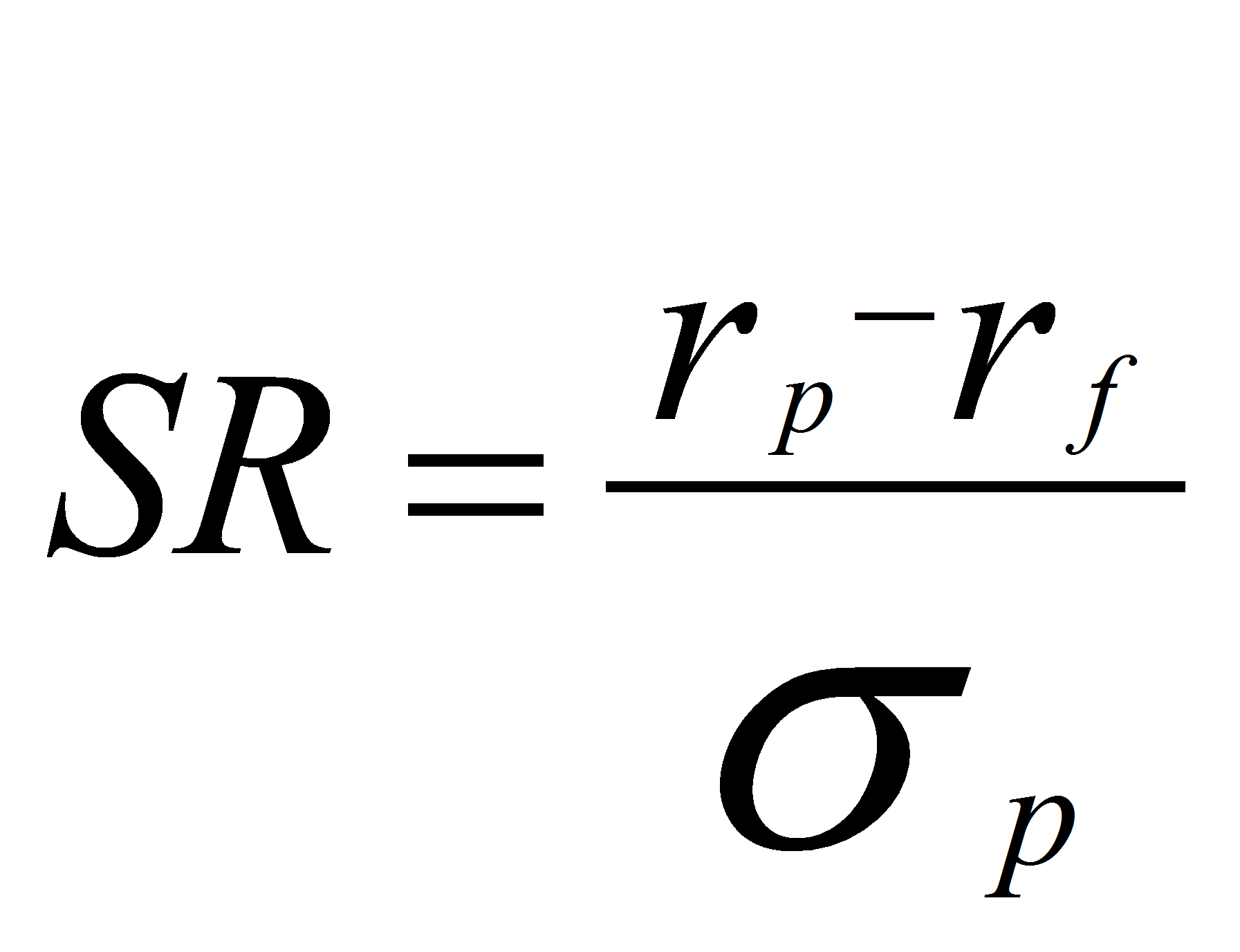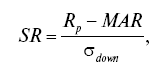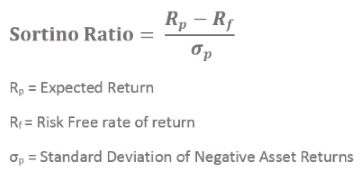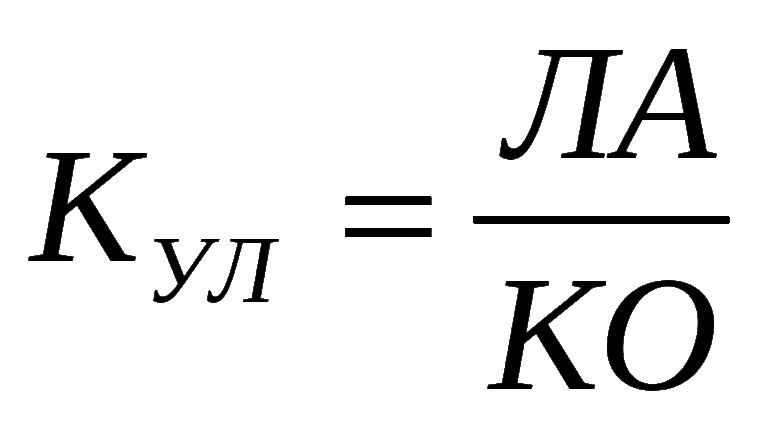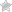Коэффициент шарпа

Усовершенствованный коэффициент Шарпа

Выше речь шла о простом коэффициенте Шарпа, а любая упрощенная формула несовершенна. Потому существующая формула была усложнена с целью сделать расчет рисков еще более точным. Сразу предупрежу: её понимание требует знаний математической статистики и рекомендуется только в случае необходимости принятия стратегически важных решений в отношении оценки портфеля ценных бумаг (к форексу данная формула не применяется). Расчет риска в формуле основывается не только на стандартном отклонении, но и на видоизмененной мере риска, позволяющей сделать оценку будущих потерь с большей реалистичностью благодаря анализу характера распределения исторической прибыльности.

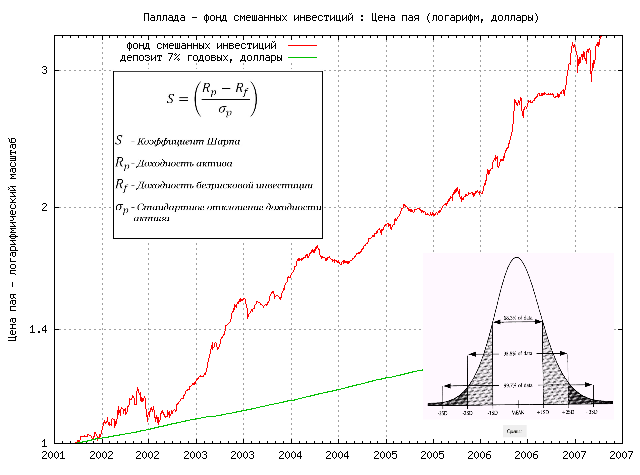
Формула усовершенствованного коэффициента Шарпа:

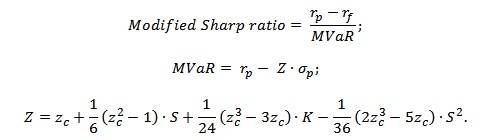
r_p — усредненная прибыльность портфеля ценных бумаг, r_f — усредненная прибыльность безрискового актива, σ_p— стандартное математическое отклонение прибыльности портфеля ценных бумаг, S — эксцесс распределения доходности, z_c — куртозис распределения прибыльностей портфеля, К — квантиль распределения прибыли.

Всем, кому слова «куртозис» и «квантиль» ни о чем не говорят, «Добро пожаловать» в эконометрику и математическую статистику. Глубоко копать в рамках этой статьи не вижу смысла, т.к. большинству будет достаточно общей информации.

Смотрите также

Расчет доходности безрискового актива

Для оценки избыточной доходности, которую получил инвестор необходимо рассчитать минимальную возможную доходность, которую он мог бы получить при вложении в абсолютно надежные активы. Именно избыточная доходность отражает качество управления и эффективность принимаемых решений менеджером паевого инвестиционного фонда.

Существуют несколько способов оценки доходности безрискового актива:

Доходность банковского вклада наиболее крупных и надежных банков РФ. К таким банкам можно отнести Сбербанк, Альфа-банк, ВТБ 24.
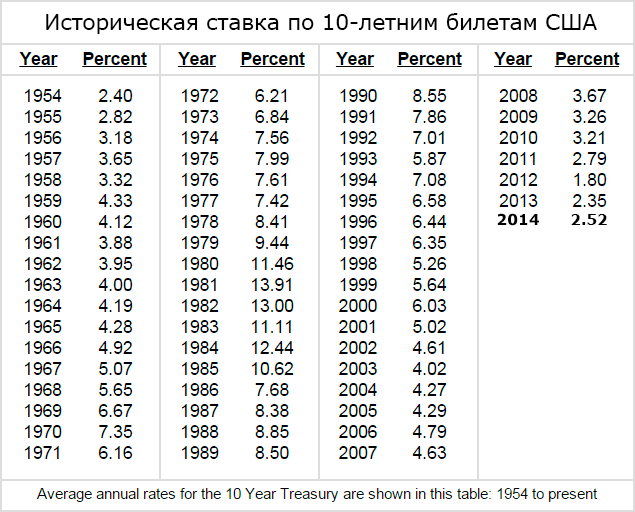
Доходность безрисковых государственных ценных бумаг (ГКО, ОФЗ в России, 10 летние облигации для США), которые обладают максимально возможной надежностью по рейтингам международных рейтинговых агентств Moody’s, Standard&poor’s и Fitch.

В результате необходимо сопоставить доходность полученную за счет управления рискованными ценными бумагами и минимальный уровень доходность абсолютно надежного актива.

Что такое Коэффициент Шарпа?

Коэффициент Шарпа — это показатель, используемый инвесторами для лучшего понимания возврата инвестиций на единицу риска.

Это соотношение позволяет инвесторам определить, какую часть прибыли они получат в зависимости от волатильности, которую они будут испытывать при удержании актива.

Это означает, что актив или портфель с более высоким коэффициентом Шарпа рассматривается как лучший выбор по сравнению с другими инвестициями в той же категории.

Такое более высокое соотношение просто приводит к высокой доходности при минимальном риске инвестиций.

Государство и общество

История

В 1952 году Артур Д. Рой предложил максимизировать соотношение «(md) / σ», где m — ожидаемая валовая прибыль, d — некоторый «уровень катастрофы» (также известный как минимально допустимая доходность или MAR), а σ — стандартное отклонение доходности. . Этот коэффициент представляет собой просто коэффициент Шарпа, только с использованием минимально допустимой доходности вместо безрисковой ставки в числителе и использования стандартного отклонения доходности вместо стандартного отклонения избыточной доходности в знаменателе. Коэффициент Роя также связан с коэффициентом Сортино , который также использует MAR в числителе, но использует другое стандартное отклонение (полу / нижнее отклонение) в знаменателе.

В 1966 году Уильям Ф. Шарп разработал то, что сейчас известно как коэффициент Шарпа. Первоначально Шарп называл это соотношением «вознаграждение / вариативность», прежде чем его стали называть коэффициентом Шарпа более поздние ученые и финансовые операторы. Определение было:

Sзнак равноEр-ржvарр.{\ displaystyle S = {\ frac {E } {\ sqrt {\ mathrm {var} }}}.}

В редакции Шарпа от 1994 года признается, что за основу для сравнения должен лежать применимый эталон, который со временем меняется. После этой редакции определение выглядит следующим образом:

Sзнак равноEр-рбvарр-рб.{\ displaystyle S = {\ frac {E } {\ sqrt {\ mathrm {var} }}}.}

Обратите внимание: если R f — постоянная безрисковая доходность в течение периода,

vарр-ржзнак равноvарр.{\ displaystyle {\ sqrt {\ mathrm {var} }} = {\ sqrt {\ mathrm {var} }}.}

В последнее время (исходный) коэффициент Шарпа часто подвергается сомнению в отношении его пригодности в качестве показателя эффективности фонда в периоды оценки падающих рынков.

Расчет модели CAPM в Excel

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

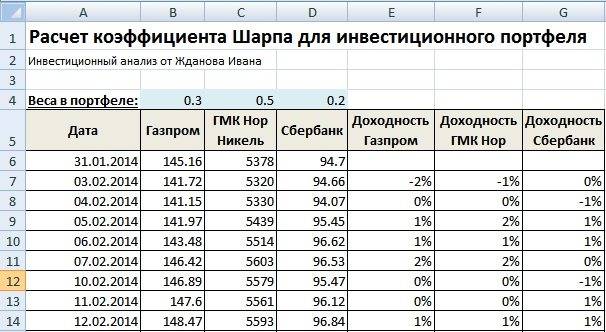
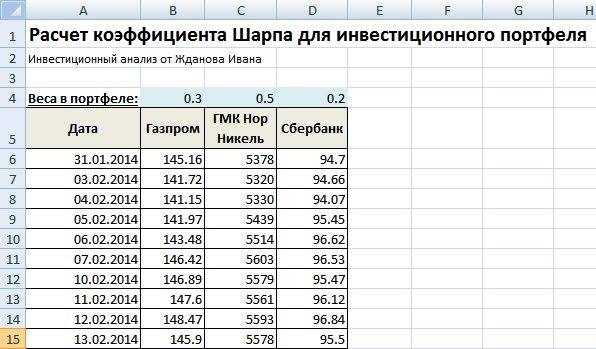
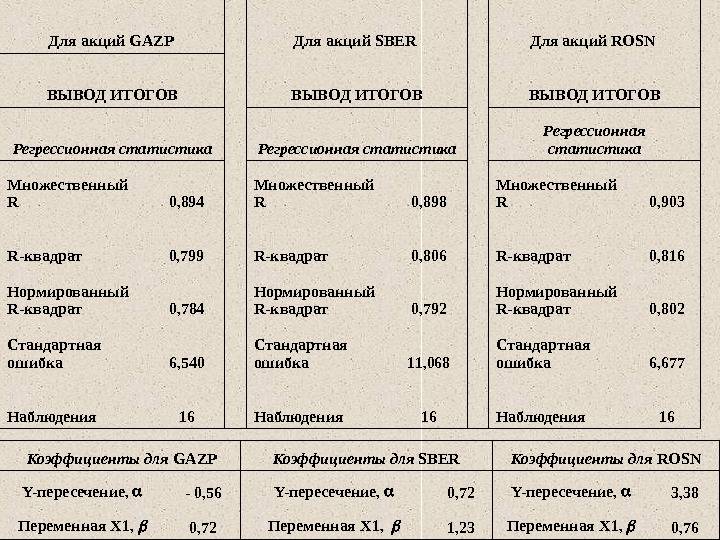
Для того чтобы лучше понять модель CAPM разберем ее на реальном примере акций предприятия ОАО «Газпром». Для этого воспользуемся программой Excel. Получить котировки акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных».

В нашей формуле за рыночную доходность будем брать изменения индекса РТС (RTSI), также это может быть индекс ММВБ (MICECX). Для американских акций зачастую берут изменения индекса S&P500. Были взяты ежедневные котировки акции и индекса за 1 год (250 данных), начиная с 31.01.2014 по 30.01.2015 г.
Далее необходимо рассчитать доходности акции (E) и индекса (D), по формулам:

=(B7-B6)/B6

=(C7-C6)/C6

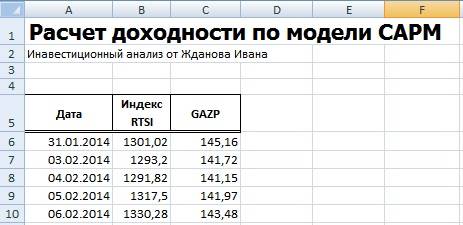
Хочется заметить, что для оценки доходностей могла быть использована также формула расчета через натуральный логарифм:

=LN(B7/B6)

=LN(C7/C6)

Итоговый результат расчета доходности одинаковый.

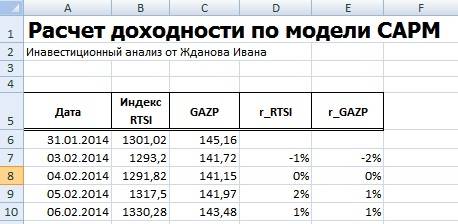
На следующем этапе необходимо рассчитать значение коэффициента бета, отражающего рыночный риск акции. Для этого есть два варианта расчета.

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

Расчет коэффициента бета с помощью формул Excel

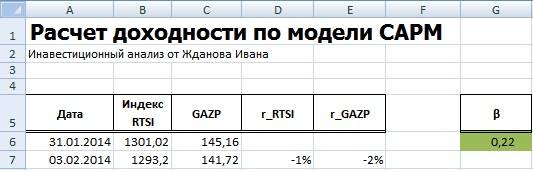
Для расчета коэффициента бета можно воспользоваться формулой ИНДЕКС и ЛИНЕЙН, первая позволяет взять индекс b из формулы линейной регрессии между доходностями акции и индекса, который соответствует коэффициенту бета. Формула расчета будет следующая:

=ИНДЕКС(ЛИНЕЙН(E7:E256;D7:D256);1)

Расчет коэффициента бета через надстройку «Регрессия»

Второй вариант расчета рыночного риска модели заключается в использовании надстройки в разделе «Главное меню» → «Данные» →«Анализ данных» → «Регрессия».

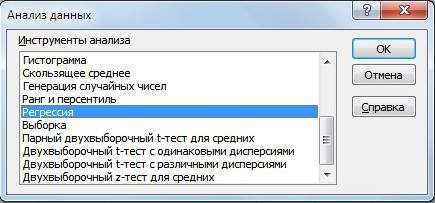
В открывшемся окне необходимо заполнить два поля: «Входной интервал Y» и «Входной интервал Х» доходностями индекса и акции соответственно.

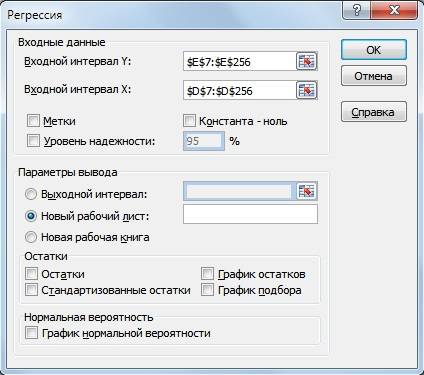
На новом листе Excel появится основные параметры модели линейной регрессии. В ячейке В18 отразится рассчитанный коэффициент линейной регрессии – коэффициент бета. Рассмотрим другие полученные параметры анализа. Так показатель Множественной R (коэффициента корреляции) между доходностью акции и индекса составляет 0,29, что показывает низкую степень зависимости доходности акции от доходности индекса. Коэффициент R-квадрат (коэффициент детерминированности) отражает точность полученной модели. Точность составляет 0,08, что очень мало для того чтобы принимать адекватные решения о прогнозировании будущей доходности на основе взаимосвязи только с уровнем риска рынка.

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут(расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR)
+ прогнозирование движения курса

Что показывает коэффициент бета в модели CAPM?

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

Коэффициент бета показывает чувствительность изменения доходности акции и доходности рынка. Другими словами, отражает рискованность вложения в тот или иной актив. Коэффициент бета служит мерой рыночного риска. Знак перед показателем отражает их однонаправленное или разнонаправленное движение. Рассмотрим более подробно значение бета в таблице ниже:

Значение коэффициента бета	Комментарии
β > 1	Доходность акция более чувствительная к изменению, доходности рынка
β = 1	Доходность акции совпадает доходности рынка
0 < β < 1	Доходность акции менее чувствительна к изменениям доходности рынка
β = 0	Доходность акции не зависит от доходности рынка полностью

В нашем примере, мы получили значение бета равной 0,22 – это показывает малую степень влияния рыночного риска на доходность акции ОАО «Газпром». На следующем этапе необходимо рассчитать безрисковую ставку (r_f).

Пройдите наш авторский курс по выбору акций на фондовом рынке → обучающий курс

Расчет средней доходности рынка (индекса РТС) проходит простой формуле Excel:

=СРЗНАЧ(D6:D256)

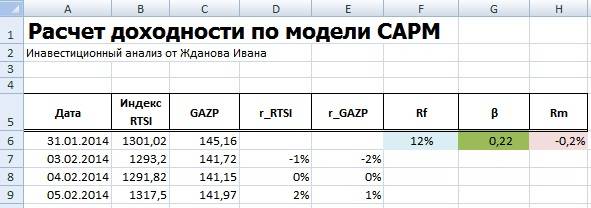
Расчет будущей доходности по модели CAPM

Рассчитаем будущую доходность акции ОАО «Газпром» на основе модели CAPM (R_capm). Формула оценки следующая:

=F6+G6*(H6-F6)

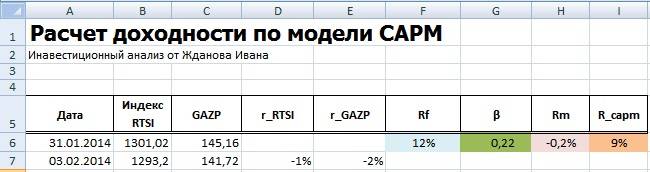
Как мы видим, что по модели CAPM ожидается доходность акции ОАО «Газпром» в размере 9%, что ниже, чем доходность по безрисковому активу. Доходность рынка составила отрицательное значение (-0,2%). Это объясняется тем, что сейчас наблюдается кризис на фондовом рынке, что приводит к оттоку капитала и созданию неустойчивой инвестиционной среды. Современные методы оценки инвестиций и инвестиционных портфелей вы можете прочитать в моей статье: “Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel“.

Коэффициент Шарпа – расчет и примеры на Форекс и фондовом рынке

Начиная торговать на фондовом рынке или на рынке Форекс, стоит оценить разумность вложений в выбранную валютную пару или фьючерс. В этом вопросе так же поможет коэффициент Шарпа. Для наглядности давайте рассмотрим примеры.

Пример расчета коэффициента Шарпа

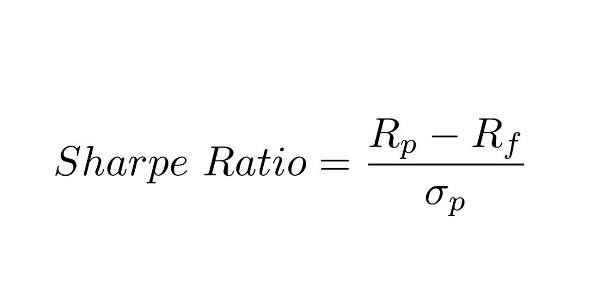
Для того, чтобы выбрать из двух стратегий, оценивать их эффективность будем при помощи коэффициента Шарпа.

Например, при торговле на рынке forex доходность первой стратегии составляет 8% при коэффициенте отклонения 5%. Есть еще одна стратегия с доходностью 6% и стандартным отклонением 2%. На первый взгляд, кажется, что первая стратегия привлекательнее, ведь доходность по ней выше на 2 %. Однако, рассчитав коэффициент Шарпа (КШ), видим следующее:

КШ первой стратегии=8/5=1,6
КШ второй стратегии=6/2=3
Таким образом, сравнив значения показателя Шарпа, видим, что вторая стратегия менее рискованная, хотя доходность немного ниже.

Существует много встроенных инструментов, в которых уже посчитаны основные коэффициенты. Давайте рассмотрим расчет Шарпа на реальном примере. Например, вы решили купить акции Сбербанка. Средняя волатильность акций составляет 2,4% в день при доходности 10,72% в месяц или 0,357% в день. Используя эти данные, подставим их в формулу и получим следующий результат:

КШ = 0,357%/2,4%=0,1485. Достаточно низкий коэффициент, что говорит о высоком риске инвестирования. Стоит отметить, что волатильность, то есть колебания цены, может быть ниже в долгосрочном периоде.

Каким должен быть коэффициент Шарпа на Форекс

Итак, вы провели все необходимые действия и рассчитали значение коэффициента Шарпа. Но без понимания, как его применять, это бессмысленно. Каким должен быть этот показатель на рынке Форекс?

Значение коэффициента 1 и больше – стратегия эффективна с точки зрения соотношения риска и доходности.
Показатель лежит в диапазоне от 0 до 1 – в данном случае существуют повышенные риски при заключении сделки, но все же стратегию можно использовать.
Отрицательное значение коэффициента говорит о том, что доходность ничтожна в сравнении с риском, на который придется пойти инвестору, чтобы заработать. Разумно отказаться от такой торговли, чтобы не потерять деньги.

Применение коэффициента Шарпа на фондовых рынках

При торговле на фондовых рынках широко применяется анализ с использованием вычисления коэффициента Шарпа. Важным нюансом является то, что безрисковая доходность отсутствует.

Следующим шагом является определение уровня риска. При торговле на фондовых биржах в качестве данного параметра используется волатильность актива за тот же временной интервал, что и доходность. Волатильность можно определить через калькулятор волатильности, используя сервисы брокеров или торговые терминалы. Использовать калькулятор очень просто достаточно задать временной промежуток и система выведет на экран список активов, где напротив каждой валютной пары будет указано искомое значение.

Далее необходимо разделить значение доходности на показатель риска. Полученная в результате выполненных действий цифра и будет коэффициент Шарпа.

Коэффициент Шарпа при инвестициях в ПАММ-счета

Если вы решили инвестировать, используя ПАММ-счет, то перед вами встанет выбор управляющего. В этом случае очень полезно использование коэффициента Шарпа для сравнения нескольких управляющих ПАММ-счетами.

Возьмем результаты торговли двух счетов. Например трейдеры А и Б показывают одинаковую доходность при совершении сделок 30%. Кого из них выбрать? Определяем значение коэффициента Шарпа для каждого из них. Для этого достаточно перейти в личную информацию трейдера, где мы возьмем данные по стандартному отклонению от доходности. Например, у управляющего А этот показатель равен 20,2%, а у Б 28,3%. Теперь определим, что менее рискованным будет вклад, открытый под 12% годовых. Подставляем параметры в формулу, получаем:

S (А) = (30%-12%)/20,2%=0,39%
S (Б)= (30%-12%)/28,3%=0,28%

Исходя из полученных информации, наглядно видно, что трейдер А рискует меньше, чем Б. То есть, способ торговли управляющего А является более эффективным и безопасным при той же доходности, в отличие от Б.

Рыночные и нерыночные риски

Рисков великое множество. Для лучшего понимания приведу одну из возможных классификаций рисков, чтобы понимать, какие опасности подстерегают частного инвестора на финансовых рынках.

Риски могут быть рыночными и нерыночными. Примеры нерыночных рисков я приводила выше — стихийные бедствия, мошенничество, операционные ошибки, судебное преследование и многое другое. Эти риски сложно оценить, действие их чаще всего весьма разрушительно, а, порой, и фатально. То есть это неблагоприятные события с маленькой вероятностью и с потенциально огромным ущербом.

А теперь поговорим о рыночных рисках и о том, как их учитывать простому инвестору при оценке эффективности управления портфелем.

Рыночные риски связанны с рыночной конъюнктурой, в том числе с ценовыми, курсовыми, валютными, процентными рисками и риском ликвидности.

Риски можно попытаться измерить. А так как риск — результат неопределенности, то и измеряться он будет вероятностью наступления того или иного события.

Вопрос измерения риска совсем не простой и точно не для этой статьи. В этой статье я хотела рассказать о показателях, оценивающих эффективность управления портфелем ценных бумаг с учетом риска.

Полезные статьи:

Коэффициент Сортино

Решить проблему, обозначенную в пункте 2, призван коэффициент Сортино, который по сути является модернизированным предыдущим показателем. Тут вместо стандартного отклонения в знаменателе используется отклонение в отрицательную сторону (ниже безрисковой процентной ставки), что позволяет учесть влияние лишь отрицательной волатильности. Логичность такого подхода признавал и уже упомянутый выше Марковиц, а на практике его воплотил Френк Сортино в 80-х годах.

где

R — доходность торговли за период

T — доходность безрискового инструмента за период

σ — отрицательная волатильность:

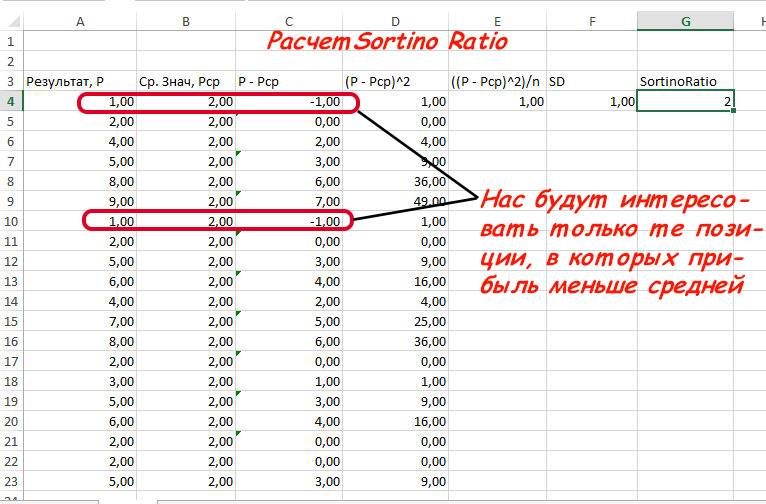
Рассмотрим годовую торговлю, где трейдер по кварталам показал результаты 26%, 10%, 1% и 3%. Тогда средняя доходность равна:

R = (26% + 10% + 1% + 3%)/4 = 10%

Годовая ставка по депозиту пусть будет равна 6% и числитель формулы в этом случае (R–T) = 10% — 6% = 4%. Для расчета знаменателя нужно учесть только те значения, которые меньше безрисковой ставки, т.е в данном случае меньше 6%. Это 1% и 3%. При этом, однако, результат делится на общее число замеров доходности, т.е. на четыре:

σ = √(((6-1) × (6-1) + (6-3) × (6-3)) /4) = 2,915%

Следовательно, коэффициент Сортино равен

S = 4/2.915 = 1.37

Хорошим результатом можно считать значение больше 0.5. Если результат считается на полгода, то доходность безрисковой ставки нужно делить на два, за три года — умножать на три и пр. Интересно, что согласно формулам коэффициенты Шарпа и Сортино при равенстве доходности торговли и безрисковой ставки получаются равными нулю вне зависимости от стандартного отклонения. Если результат торговли хуже безрисковой ставки, то знак коэффициентов будет отрицательным.

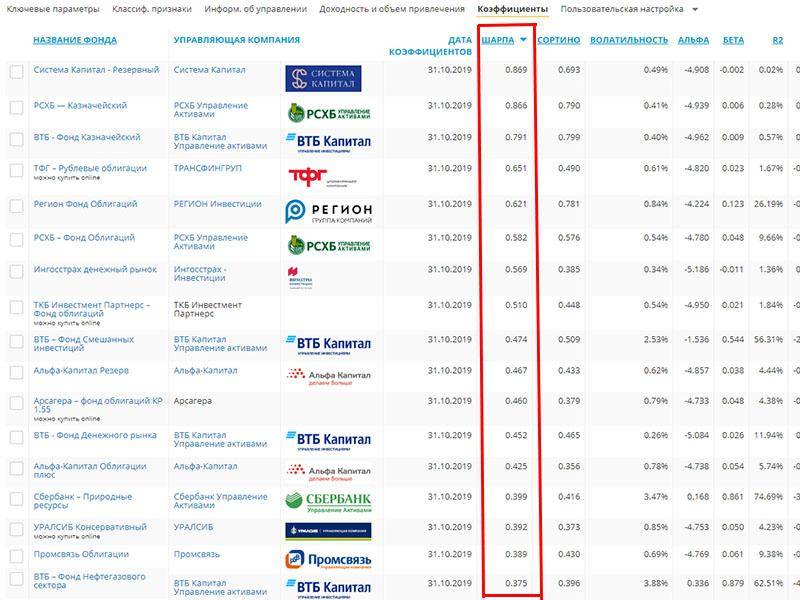
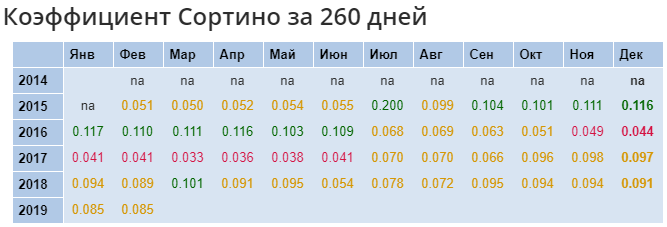
Посмотреть данные по конкретному фонду можно на сайте investfunds.ru, найдя нужный вариант и там «Аналитические коэффициенты». На том же сайте есть и методика расчета коэффициентов, из которой следует, что вычисления производятся на ежемесячной основе для открытых и интервальных фондов со статистикой за последние 36 месяцев.

Инфографика. Коэффициент Шарпа (основные моменты)

Недостатки коэффициента Шарпа

Одним из недостатков коэффициента Шарпа является использование стандартного отклонения доходности для измерения доходности инвестиций.

Стандартное отклонение основано на предположении, что доходы распределяются равномерно. Однако трейдеры и инвесторы знают, что ценовые движения на финансовых рынках не всегда распределяются равномерно в течение определенного периода времени.

В некоторые торговые дни наблюдается значительный всплеск из-за какого-то случайного события. В другие дни рынок находится в минусе из-за того, что трейдеры извлекают выгоду из явной возможности открывать короткие позиции на основе технических индикаторов.

Вторым недостатком коэффициента Шарпа является простая способность некоторых портфельных менеджеров манипулировать своими ресурсами для укрепления своей репутации. Это можно сделать, используя более длительный период времени для измерения волатильности, что приводит к снижению значения.

Портфельный менеджер может принять решение использовать стандартное отклонение в течение нескольких месяцев, а не нескольких дней. Первый набор данных обеспечивает более низкую оценку волатильности по сравнению со вторым.

В-третьих, управляющий портфелем может принять решение о выборке данных за период времени, когда волатильность была однородной или отсутствовала. Таким образом, преднамеренно выбирая набор данных, менеджер портфеля может искажать окончательное значение коэффициента Шарпа для своей выгоды.

Сущность показателя

Коэффициент Шарпа показывает работоспособность используемой торговой стратегии или финансового инструмента. Чем он выше, тем более эффективен объект оценки.

Данные этого коэффициента показывают как показатель прошлых оценок прибыльности к риску, так и прогнозируют уровень стабильности потенциальной прибыли. В связи с этим он чаще всего применяется финансовыми аналитиками в сводных таблицах, в которых приводится оценка активов.

Литература

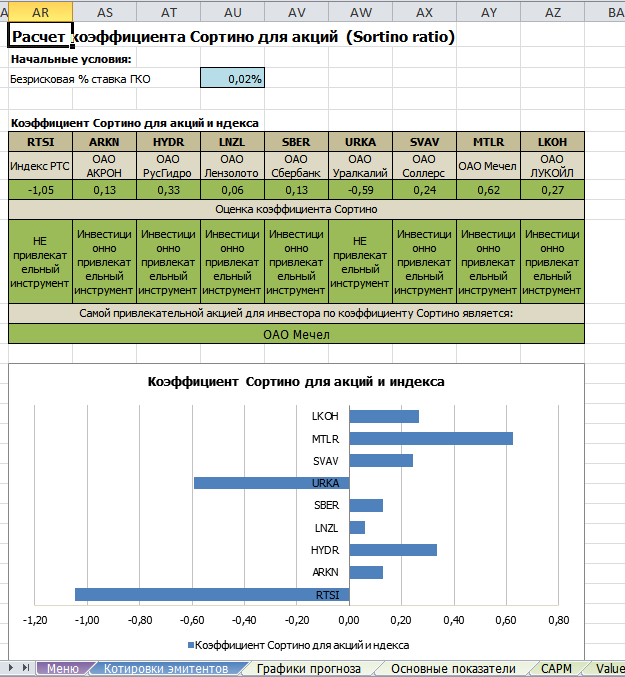
Оценка коэффициента Сортино для иностранных инвестиционных портфелей

Одним из лучших портфельных анализаторов по составлению портфеля является онлайн сервис – Portfoliovisualizer.com и его сервис “Backtest Portfolio Asset Allocation” (находится во вкладке Tools). На картинке представил базовые установки, которые я не меняю

Опции на которые необходимо обратить дополнительное внимание – это:

Ребалансировка (Rebalancing: годовая, квартальная месячная) – перекладывание между активами для сохранения первоначальной пропорции портфеля. Например, если у нас есть портфель, состоящий из 70% акций и 30% облигаций, при росте акций необходимо часть прибыли зафиксировать и вложить в облигации. Приведя соотношение капитала к первоначальным условиям.
Денежный поток (Cash Flow) – это сумма, которая будет вноситься за выбранный период (месяц, квартал, год) в дополнение к первоначальным инвестициям. Есть опция добавить учет инфляции.
Бенчмарк (Benchmark) – опция для сравнения с доходностью созданного портфеля, индекса S&P500 или с доходностью одного из успешнейших фондов Vanguard 500 Index.

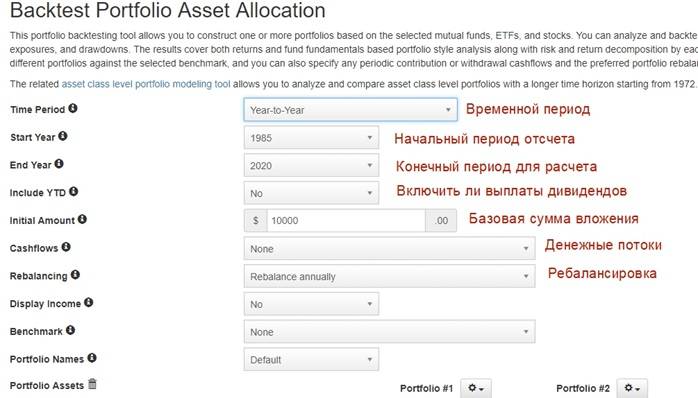
Базовые опции сервиса по созданию и оценки эффективности инвестиционных портфелей для зарубежного рынка

На следующем этапе необходимо составить портфель из активов (акций, облигаций, ETF, REIT). Сумма по всем активам должна быть 100%. Существует способ для того, чтобы на основе оптимизации определить доли активов в портфеле, которые максимизируют его доходности или минимизируют риск. В данной статье я взял равные доли активов, чтобы показать принцип построения и оценки по коэффициенту Сортино.

Для формирования портфеля были взяты лидеры технологического сектора: акции компаний: Google (GOOGL), Apple (AAPL), Amazon (AMZN), Alibaba (BABA).

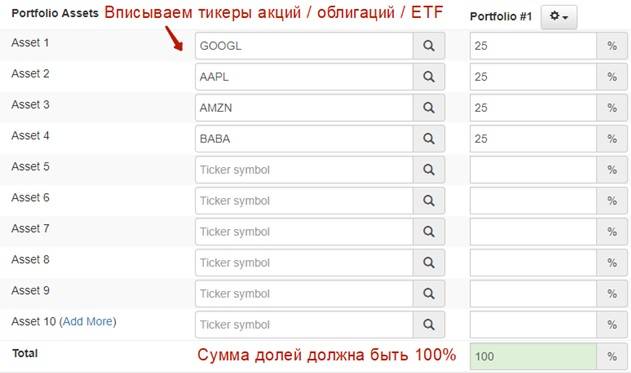
Включение в портфель акций технологических компаний

Итог будет сравнение сформированного портфеля и выбранного бенчмарк (Vanguard 500 Index).

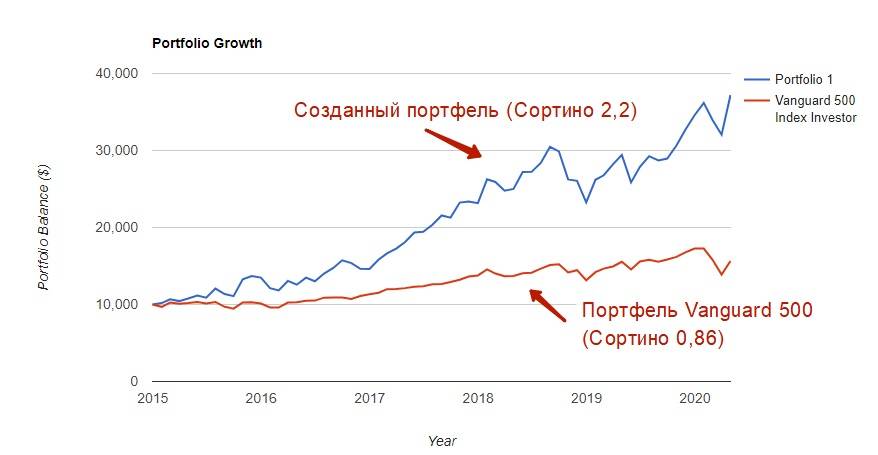
График доходности инвестиционного портфеля и бенчмарка (Vanguard 500)

Важным моментом сравнения будет оценка коэффициентов эффективности портфелей и их показателей Сортино. В результирующей таблице показано, что Сортино у собранного портфеля лучше себя показал и увеличил инвестиции с 10 до 37 тысяч, при максимальной просадке в 23%, тогда как фонд Vanguard увеличил капитал до 15 тысяч с просадкой в -19%.

Портфели	Инвестиции	Итоговый баланс	Стандартное отклонение (риск)	Максимальная просадка	Sortino Ratio
Собранный портфель	10000$	37200$	22.26%	-23.71%	2.21
Vanguard 500	10000$	15659$	14.53%	-19.63%	0.86

Сравнивая коэффициенты Сортино ИП, мы может выбрать тот портфель, который нацелен на максимизацию доходности.

Какие бывают виды стоимости акций

Дополнительно определяются мультипликаторами различных видов — экономические показатели публичного акционерного общества, выраженные через математическую формулу. Ниже виды и способы стоимостной оценки акций.

Номинальная

Степень его участия не ограничивается консультациями. Андеррайтер берет на себя весь процесс по размещению акций на открытом фондовом рынке, включая оценку акций. Максимальная степень участия предполагает выкуп андеррайтером всего выпуска и дальнейшее его продажа инвесторам.

В процессе IPO андеррайтером совместно с заказчиком определяется первичная цена размещения. Она является номинальной и на этом этапе не будет рыночной, зависящей от спроса и предложения.

Рыночная

После проведения IPO акции начинают торговаться на фондовой бирже. В результате биржевой торговли происходит формирование текущих рыночных цен. Это автоматический процесс.

Состоит из трех основных составляющих: торговая система на серверах биржи, сервер брокера и торговая программа конечного клиента (трейдера). Приказ от трейдера поступает брокеру, программа проверяет его на соответствие условий и транслирует на биржу.

По времени это занимает доли секунды. Все заявки формируют ленту покупок и продаж с выставленными объемами. На трейдерском сленге — «биржевой стакан».

Т+2 — основной режим торгов на ММВБ для акций. Это значит, что учет купленной или проданной акции в депозитарии происходит не завтра, а на второй день после заключения сделки на бирже.

Балансовая

BVPS (воокvaluepershare). В оценке учитывается совокупный акционерный капитал за вычетом стоимости привилегированных и количества акций в обращении. Оценка цены определяется формулой деления первого показателя ко второму. Берется среднее значение акций в обороте в расчетном периоде. Причина — рыночные события могут менять количество. Например, buyback.

Соотношение балансовой стоимости к рыночной дает инвесторам точку отсчета для стоимостной оценки. Если рыночная ниже балансовой — акции компании недооценены рынком. Может служить показателем для покупки акций.

Ликвидационная

Определяется при прекращении деятельности акционерного общества. После факта прекращения работы компании определяется стоимость всех активов. Из этой величины вычитаются внешние обязательства компании, включая кредитные средства.

Из оставшейся цифры вычитаем стоимость привилегированных акций (если есть в наличии). В результате получаем ликвидационную стоимость обыкновенных акций, подлежащих к выплате акционерам.

Инвестиционная

Рыночная цена акций определяется как стоимость «здесь и сейчас». Инвестиционная — субъективное представление инвестора о цене акций по совокупности данных. В них включают выплаты дивидендов и представления инвестора о будущем росте актива в будущем. Профессиональные инвесткомпании могут оценивать одну и ту же акцию совершенно по-разному и представлять ее инвестиционную цену по своей шкале измерений.

Эмиссионная

Такая цена предлагается первым покупателям при первичном размещении акций (IPO). Непосредственно перед выходом на публичные торги. Акционерная компания совместно с андеррайтером определяет эмиссионную стоимость и предлагает заинтересованным инвесторам купить пакет по такой цене.

Стандартный порядок подразумевает шаги:

Перед началом публичных торгов на фондовой бирже определяется эмиссионная цена.
Она официально объявляется, начинают приниматься заявки на покупку акций по этой цене. Есть даты начала приема и его окончание.

Расчетная

Необходима и для непубличных акционерных обществ в бухгалтерских расчетах. В РФ порядок определения расчетной цены ценных бумаг, не обращающихся на рынке ценных бумаг, определен налоговым кодексом и Приказом ФСФР от 09 октября 2010 г. № 10-66\пз-н. Цитата п.4 (источник — Консультант Плюс):

Некоторые специалисты допускают использование определения расчетной цены аналогично балансовой.

МСФО IFRS 9 — Факторинг дебиторской задолженности по МСФО (IFRS) 9

ETF — торгующиеся на бирже фонды

О биржевых фондах мы уже писали. Напомню суть: управляющая компания создает фонд, покупает в него активы по какому-то принципу и продает инвесторам доли в фонде. Инвестор, который купил акцию фонда, получает кусочек от всех активов фонда. Это удобно, потому что с помощью фондов легко создать хорошо диверсифицированный портфель из акций и облигаций.

На Московской бирже за евро можно купить акции четырех ETF:

FXDE — акции немецких компаний. Только у этого фонда базовый актив в евро, остальные ETF лишь торгуются за евро.
FXRU — еврооблигации российских компаний.
RUSB — еврооблигации Минфина и российских компаний.
RUSE — акции российских компаний.

Еще на Московской бирже есть биржевой ПИФ с обозначением AKEU, который инвестирует в акции европейских компаний и торгуется за евро.

Выбирая фонд, помните, что фонды акций могут принести более высокую доходность, чем фонды облигаций, но их риск выше. Фонды акций лучше подходят для долгосрочных инвестиций и тех инвесторов, кто спокойно относится к колебаниям цен.

На зарубежных биржах фондов в евро заметно больше. Для доступа к ним понадобится счет у российского брокера и статус квалифицированного инвестора либо счет у зарубежного брокера. Инвестиционные налоговые вычеты на иностранных биржах не действуют.

Примеры

Например, предположим, что мы анализируем два разных портфеля, которые составляют разные активы, такие как акции, валюты или криптовалюты. После тщательного анализа мы определяем, что первый портфель может обеспечить годовую доходность 20%. Тем не менее, риск понижения также значительно высок — 18%.

Для нашего второго портфеля у нас годовая доходность 7% и соответствующий риск понижения 1,25%. Используя гипотетический T-Bill с безрисковой доходностью 3%, мы получаем следующие сравнения между двумя портфелями.

	1-е портфолио	2-е портфолио
Норма прибыли	20	7
Безрисковая норма прибыли	3	3
Волатильность	18	1,25
Коэффициент Сортино	(20 — 3) / 18 = 0,94	(7 — 3) / 1,25 = 3,2

После завершения наших расчетов для определения коэффициентов Сортино становится ясно, что первый портфель несет больший риск, чем второй. Первый портфель предлагает высокий потенциал как для прибыли, так и для убытков.

Примеры

Пример 1

Предположим, актив имеет ожидаемую доходность на 15% сверх безрисковой ставки. Обычно мы не знаем, будет ли актив приносить такую прибыль; Предположим, мы оцениваем риск актива, определяемый как стандартное отклонение избыточной доходности актива , как 10%. Безрисковая доходность постоянна. Тогда коэффициент Шарпа (по старому определению) будетра-ржσазнак равно0,150,10знак равно1.5{\ displaystyle {\ frac {R_ {a} -R_ {f}} {\ sigma _ {a}}} = {\ frac {0,15} {0.10}} = 1,5}

Пример 2

В качестве примера вычисления чаще используют постфактум Шарпа-который использует понял , чем ожидается , возвращается на основе на современном определении, рассмотрим следующую таблицу еженедельных деклараций.

Дата	Возврат активов	Общая доходность S&P 500	Избыточная доходность
06.07.2012	-0,0050000	-0,0048419	-0,0001581
13.07.2012	0,0010000	0,0017234	-0,0007234
20.07.2012	0,0050000	0,0046110	0,0003890

Мы предполагаем, что актив представляет собой что-то вроде фонда акций США с большой капитализацией, который логически будет сравниваться с S&P 500. Среднее значение избыточной доходности составляет -0,0001642, а стандартное отклонение (выборка) составляет 0,0005562248, поэтому коэффициент Шарпа равен — 0,0001642 / 0,0005562248, или -0,2951444.

Пример 3

Предположим, что кто-то в настоящее время инвестирует в портфель с ожидаемой доходностью 12% и волатильностью 10%. Безрисковая процентная ставка — 5%. Что такое коэффициент Шарпа?

Коэффициент Шарпа: 0,12-0,050,1знак равно0,7{\ displaystyle {\ frac {0.12-0.05} {0.1}} = 0,7}

Недостатки коэффициентов

Необходимо знать об общих недостатках, присущих каждому из перечисленных коэффициентов.

Использование данных прошлого. Все расчеты обозначенных коэффициентов базируются на исторических данных. Получается, что эти коэффициенты выражают показатели деятельности фондов, которые были показаны ранее, и ничего не говорят о будущей ситуации.
Из первого недостатка следует второй. Так как расчет ведется на исторических данных за определенный период (обычно за 3 года), то изменения в качестве управления (как улучшение, так и ухудшение) отражаются на коэффициентах довольно медленно. Этот недостаток особенно опасен в случае ухудшения качества управления. К примеру, управляющий фондом 2 года показывал отличные результаты, затем его место занял другой управляющий с уже не такими выдающимися результатами. Коэффициенты же, рассчитанные на отрезке в три года, все равно будут говорить о том, что «в фонде высокое качество управления», хотя на деле это может быть не так.
Также недостатком данных коэффициентов можно считать то, что при их расчете под «риском» понимается волатильность инструмента. В таком определении есть своя логика, которая была высказана Марковицем: большая амплитуда колебаний, по его мысли, свидетельствует о большей непредсказуемости поведения цены. Однако мы уже не раз говорили, что для долгосрочного инвестора, который осуществляет вложения регулярно, волатильность инструмента только на пользу.

Тесты

Было предложено несколько статистических тестов коэффициента Шарпа. К ним относятся предложения, предложенные Джобсоном и Корки и Гиббонсом, Россом и Шанкеном.

Вывод

Подводя итоги, розничные и институциональные инвесторы нуждаются в надлежащем методе количественной оценки прибыли по отношению к риску при выборе инвестиционного выбора.

Прогнозирование потенциальной доходности недостаточно при оценке жизнеспособности инвестиций в течение определенного периода времени.

Коэффициент Шарпа обеспечивает лучшее представление о привлекательности инвестиций благодаря включению риска в их расчет. Это позволяет инвесторам лучше понять доходность по отношению к риску, принимаемому при владении активом.