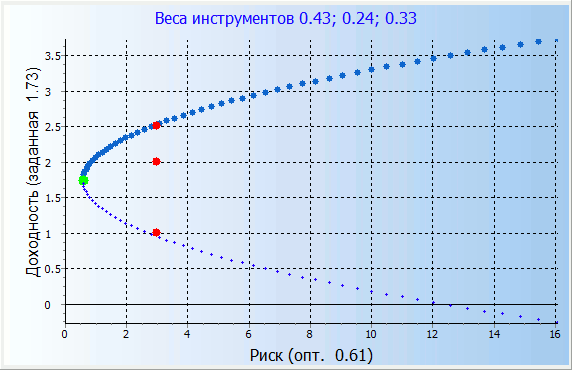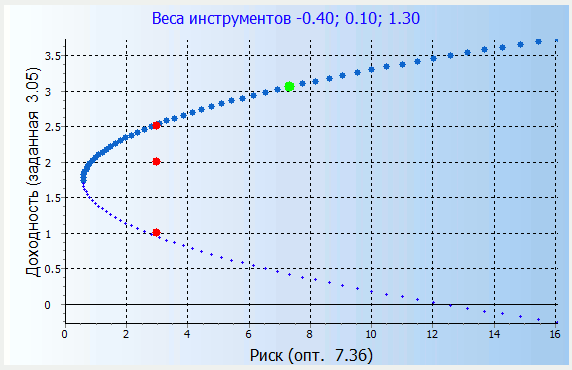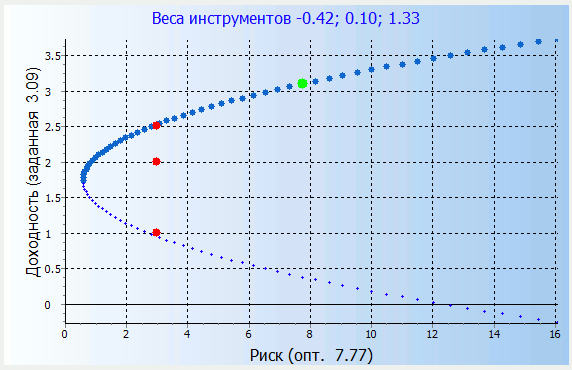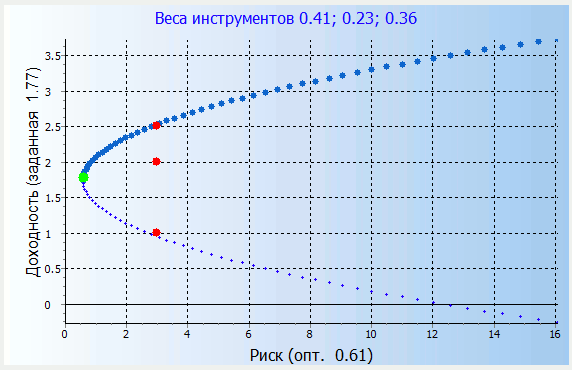
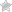Портфель Марковица
Это модель построения эффективного портфеля Марковица с использованием метода Хуанга Литценбергера в excel.
Идея модели такова: вы можете найти портфель с самым низким уровнем риска при заданной ожидаемой доходности.
Обычно можно решить задачу оптимизации портфеля использую Solver в excel. Но в таком случае вы только вводите определенные параметры и получаете ответ. Использование же подхода Хуанга Литценбергера позволяет вам увидеть расчеты. Более того, вы сможете создавать модели, в которых изменяя только ожидаемую доходность портфеля вы сразу будете получать его оптимальную структуру.
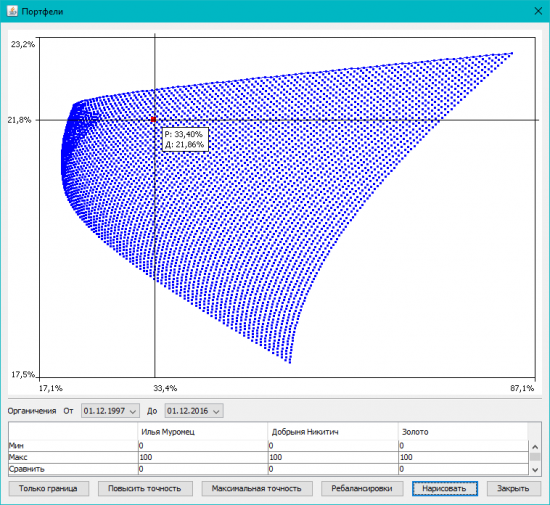
Кроме того, мы нарисуем эффективную границу.
Если вы хотите узнать больше об эффектиной границе и теории Марковица, можете посмотреть здесь
А вот ссылка на описание модели Хуанга Литценбергера.
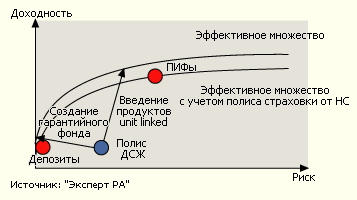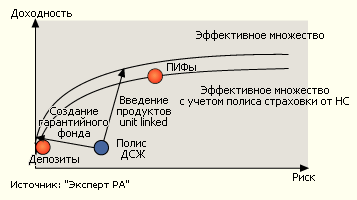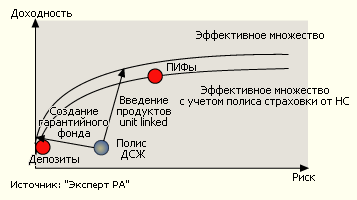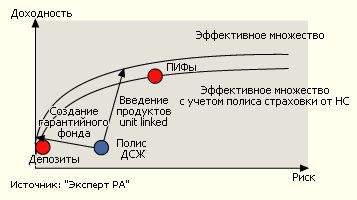
Роль диверсификации
Диверсификация – это принцип включения большого количества ценных бумаг в инвестиционный портфель, за счет чего снижается уровень его финансового риска и достигается оптимальная структура входящих активов. Такая стратегия предполагает, что показатели доходности акций будут иметь наименее возможную корреляцию, гарантируя минимальный риск и прогнозируя при этом высокую прибыль для инвестора.
Иначе говоря, мы диверсифицируем активы для того, чтобы не допускать просадки портфеля при внезапном ослаблении позиций некоторых бумаг. Например, когда доходность по одному из инструментов начинает уменьшаться, рискуя дойти до отрицательных значений, то за счет усиления позиций по другим активам общая доходность портфеля стабилизируется, снижается риск получения убытков.
Знатоки законов рынка ценных бумаг и опытные биржевые трейдеры утверждают, что оптимальное количество финансовых инструментов в портфеле – от 8 до 20, с их распределением между 2-4 классами активов (ценные бумаги, биржевые индексы, недвижимость, драгоценные металлы).
Сегодня инвесторы все чаще рассматривают в качестве инвестиционных объектов индексы, осуществить вложения в которые можно двумя способами:
- включив в портфель акции, входящие в состав индекса;
- купив ценные бумаги инвестиционных фондов, портфель которых аналогичен составу соответствующего индекса (ETF – Exchange Traded Fund).
Вложения в индексы называют пассивным инвестированием, которое решает сразу две задачи владельца портфеля – минимизация рисков за счет диверсификации и формирование сверхдолгосрочной стратегии, которая в конечном итоге принесет хорошую прибыль.
Достойную конкуренцию индексным инвестициям могут составить разве что вложения в недвижимость, в том числе трастовые фонды REIT (Real Estate Investment Trust), но они сильно проигрывают индексам по показателям ликвидности, поэтому предпочтение следует отдавать все же первым.
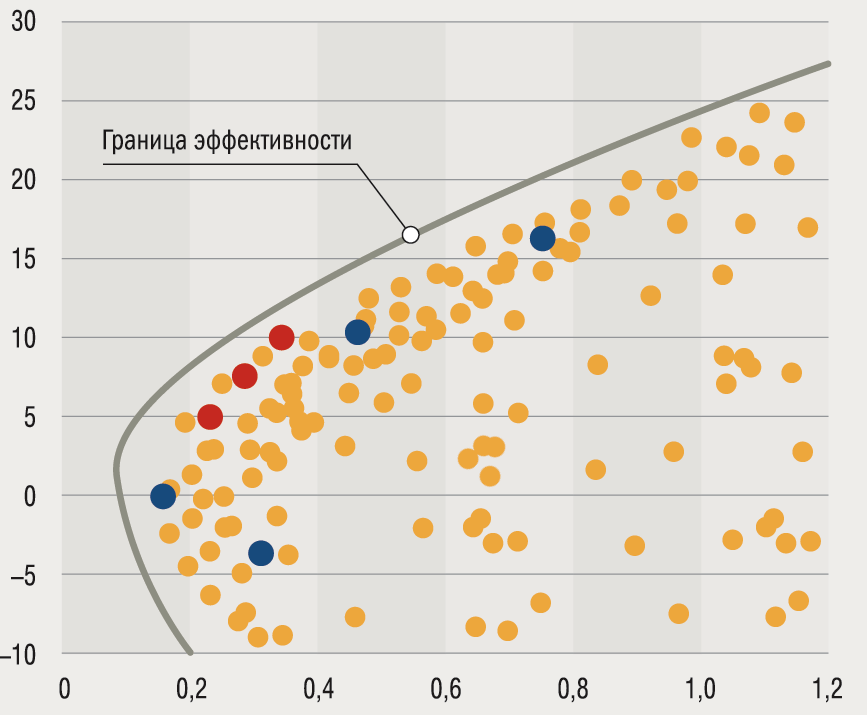
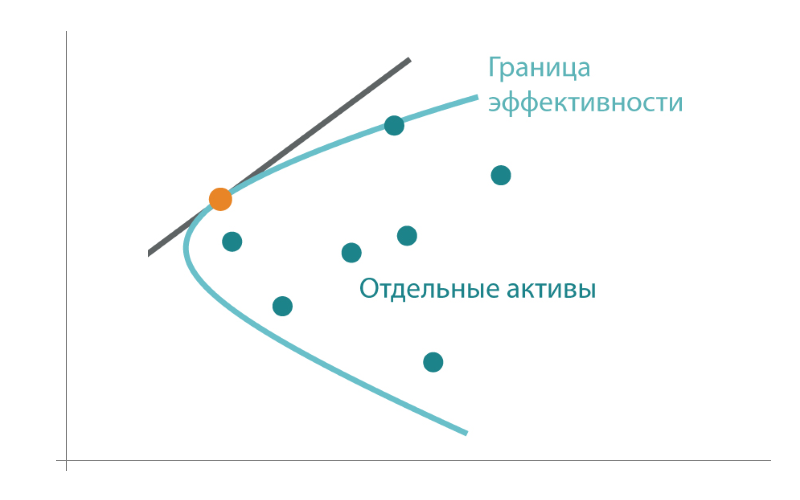
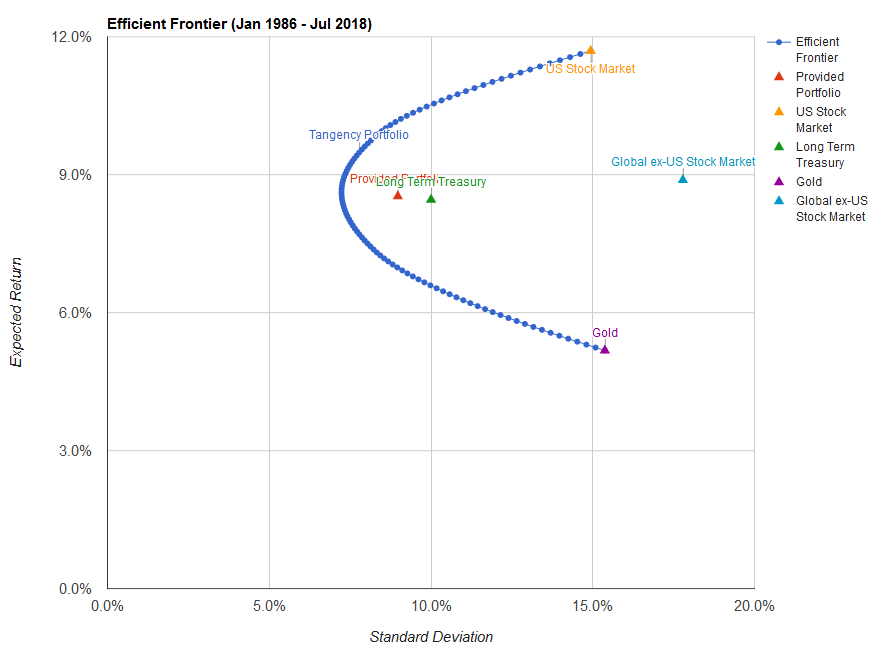
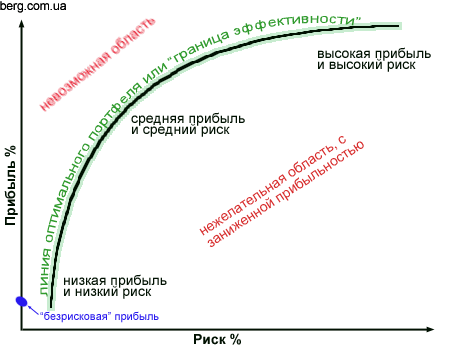
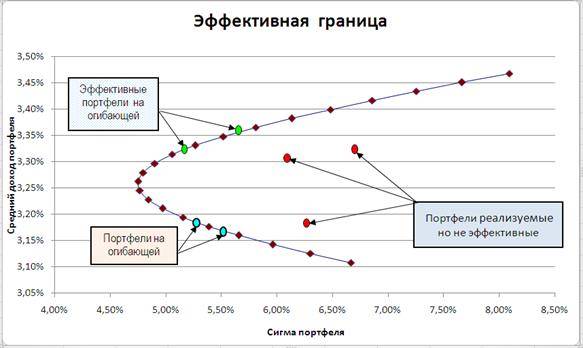
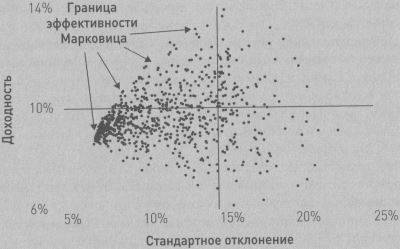
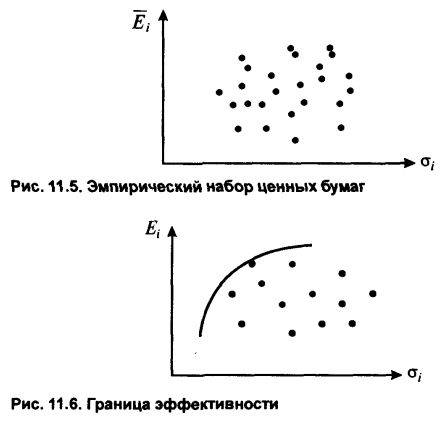
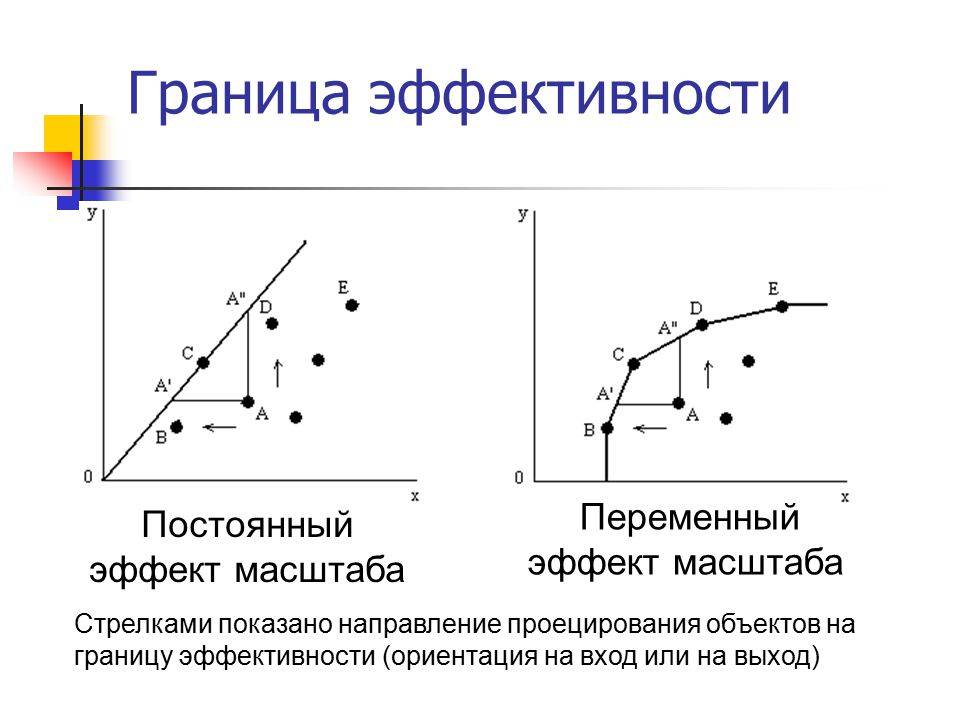
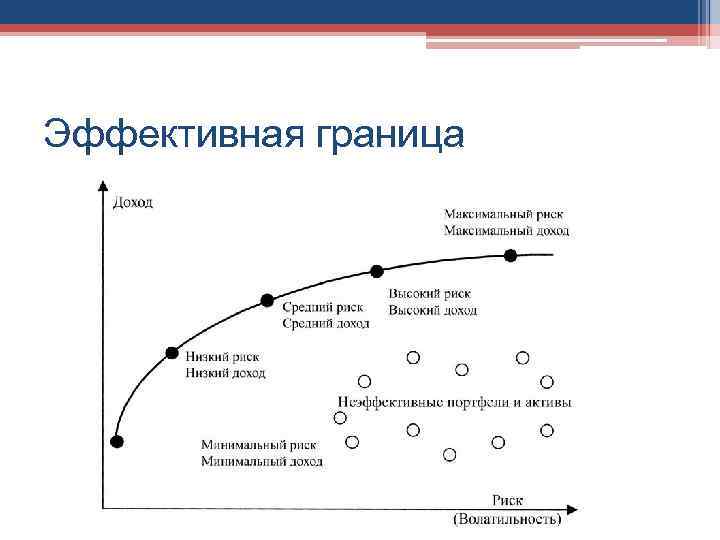
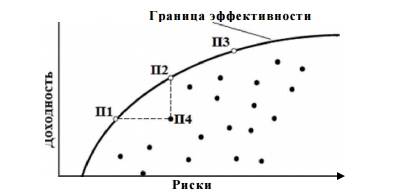
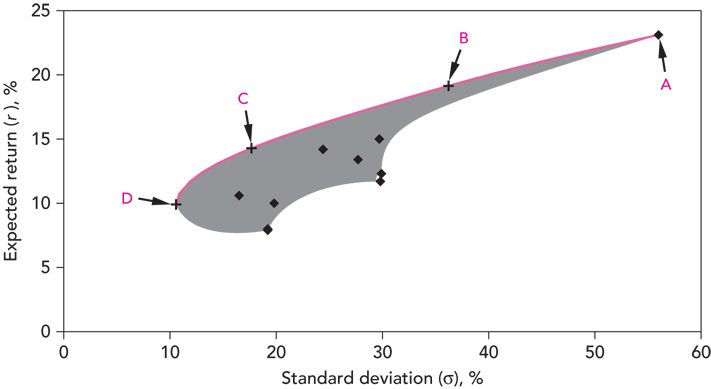
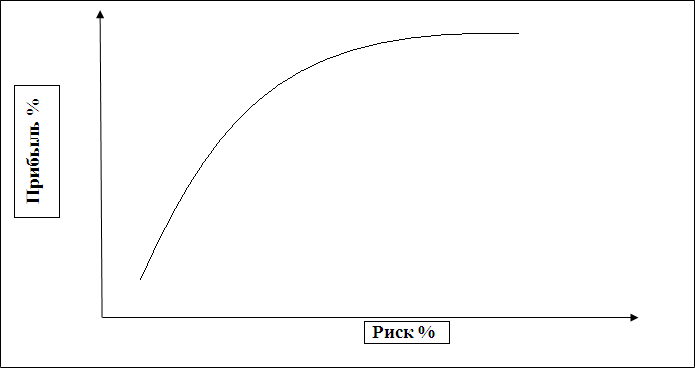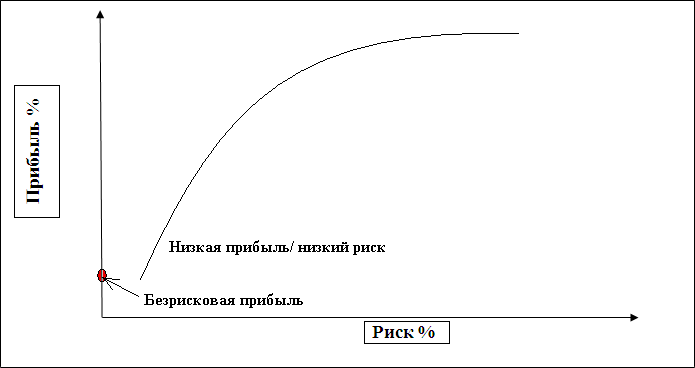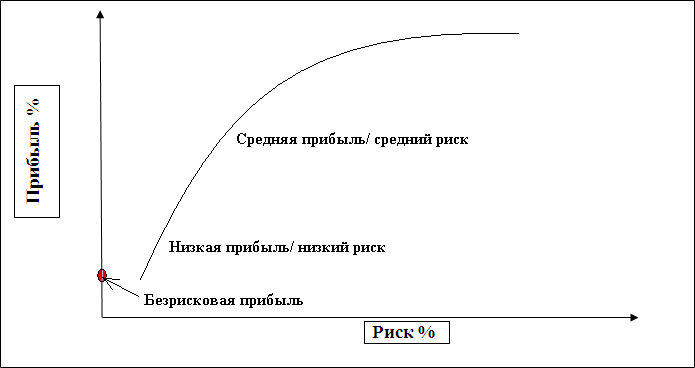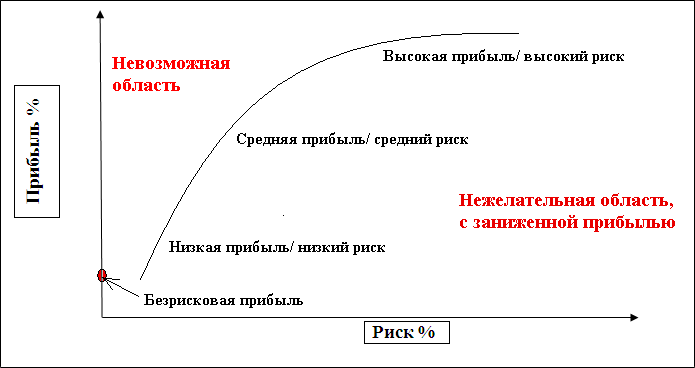
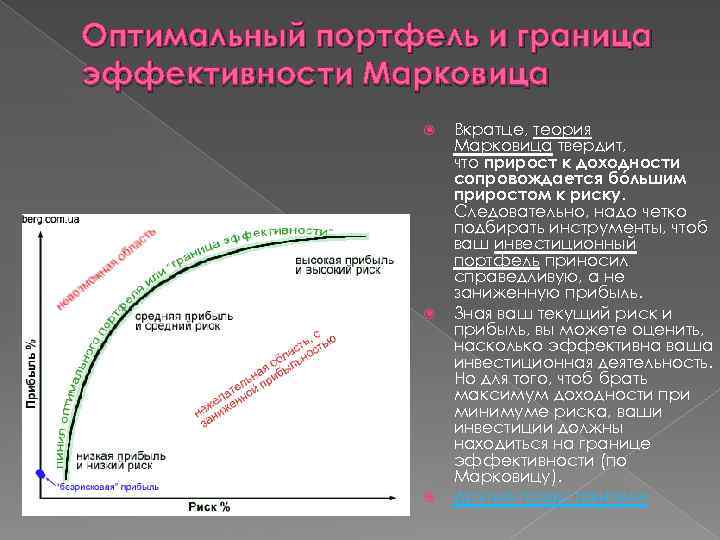
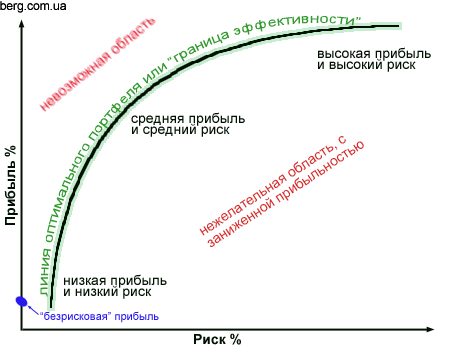
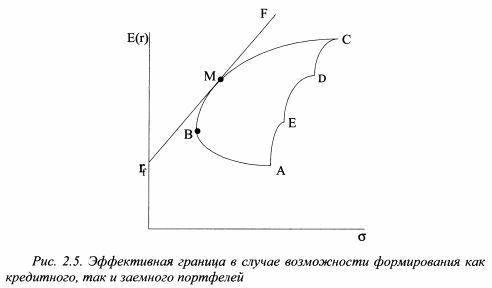
Эффективная граница
Существует функция г — Ф ( 0), график которой совпадает с эффективной границей Г ( К), причем эта функция является непрерывной, возрастающей и вогнутой.
|
Зависимость минимального риска от ожидаемой эффективности портфеля. |
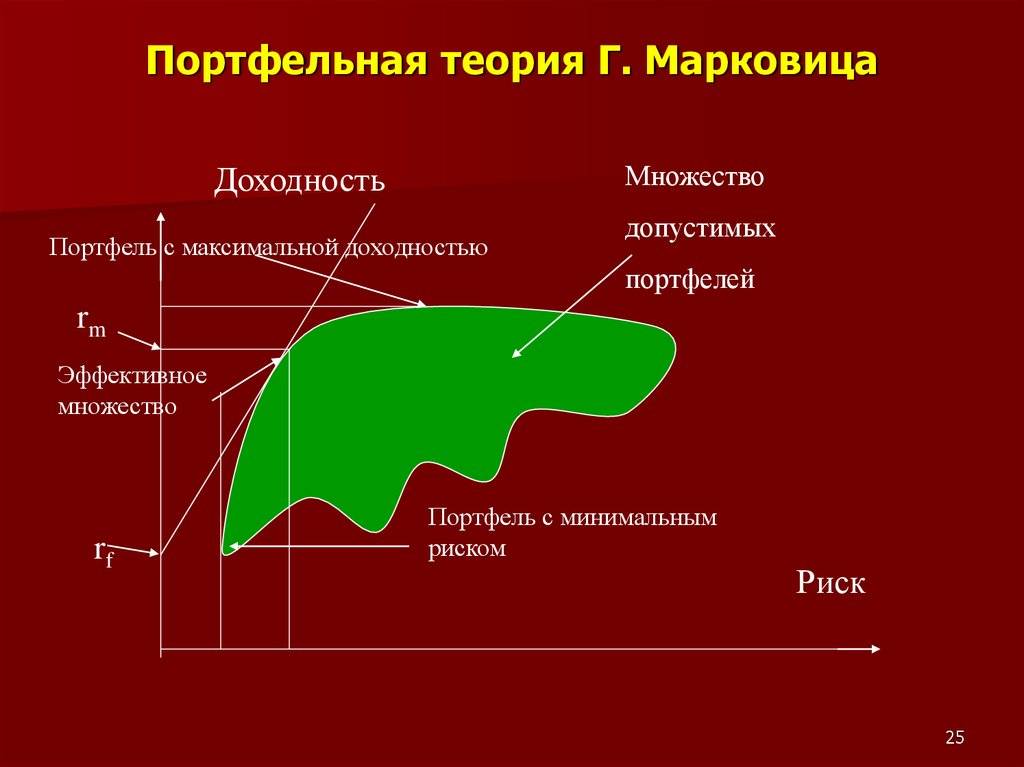
Согласно сформулированным выше принципам теории Марковица, инвестор всегда выбирает портфель, лежащий на эффективной границе. Двигаясь вдоль границы слева направо, мы увеличиваем ожидаемый риск, но при этом расширяются и границы доходности. В связи с этим возникает следующий вопрос: какой же портфель лучше. Лучший из всех портфелей на эффективной границе Марковица называется оптимальным.
Наконец, все формулы включают в себя радиус ге, который следует рассматривать как величину, определяющую внешнюю эффективную границу системы песчаник-скважина. При выводе формул этот радиус, входит как величина расстояния от центра скважины до точки, где известно давление жидкости, соответствующее Ре — давлению резервуара. С другой стороны, последнее соответствует также давлению на обнаженном забое скважины после того, как она закрыта на некоторый, достаточно долгий промежуток времени, пока в ней не будет достигнуто равновесие. Радиус ге, при котором давление жидкости в процессе фонтанирования скважины приблизительно равно давлению резервуара, заранее с достоверностью не известен. Следует заметить, что он входит в представленные формулы в логарифмическом виде. Для целей фактического подсчета достаточно принять для ге половину среднего расстояния от рассматриваемой скважины до ее ближайших соседей, за исключением тех случаев, когда дебиты последних резко отличны от рассматриваемого. Давление в срединной точке между двумя соседними скважинами приблизительно равно ( как это б ло уже определено выше) давлению резервуара.
Следует помнить, что инвестор стремится к самой высокой кривой безразличия, какую можно достичь на эффективной границе. При этих требованиях оптимальный портфель представлен точкой пересечения кривой безразличия с эффективной границей.
|
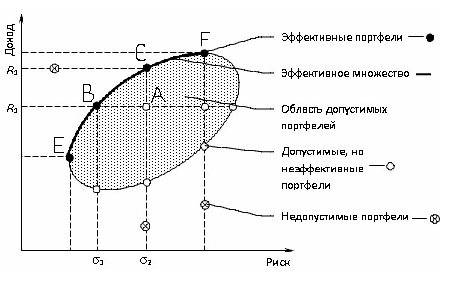
Достижимое и эффективное множества. |
Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством ( efficient set), или эффективной границей.
В экономико-математической литературе слова эффективность, эффективный используются также в составе терминов типа эффективная точка, эффективная технология, эффективная граница.
Мы покажем, что для любых данных стандартных схем R и 5 с одной переменной и засылками констант имеется эффективная граница, такая, что если R Ф S, то существует интерпретация, при которой R и 5 различаются и при этом длина истории вычислений одной из схем меньше, чем граница. Как и раньше, этого достаточно для доказательства теоремы, поскольку эквивалентность R и 5 в этом случае можно проверить выполнением схем при конечном числе конечных интерпретаций.
|
Кривые холодного сжатия железа. зависимость давления Р ( ГПа от плотности р ( г / см3 при температуре Т 0 ( сплошная линия — ХФС, штриховая линия, переходящая в сплошную при р 103 г / см3 — ТФ, пунктирная линия. |
В расчетах по методу при увеличении плотности вещества р происходят последовательные переходы дискретных уровней энергии е eni через заданную эффективную границу непрерывного спектра SQ, так как с ростом р энергии уровней растут, а граница SQ — д / Хго) снижается.
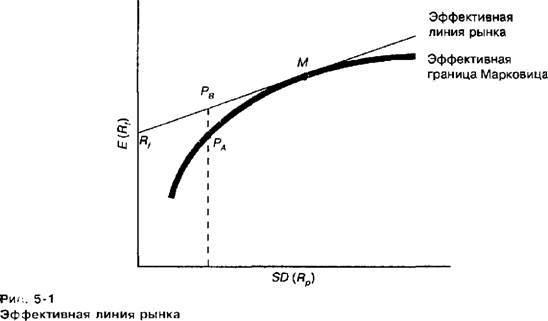
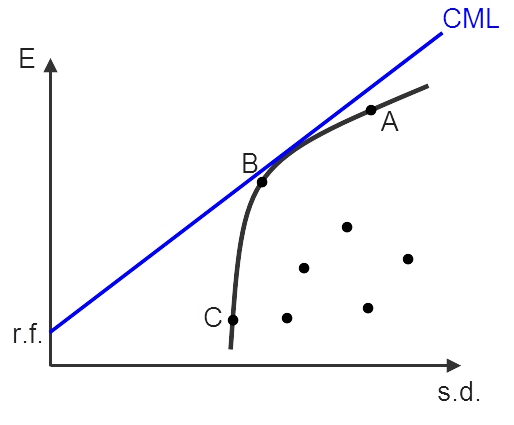
Так как эффективная граница для портфелей с неограниченной суммой весов дает один и тот же портфель с различной величиной рычага, линия CML не может пересекаться или касаться эффективной границы портфелей с неограниченной суммой весов, если же сумма весов ограничена ( т.е. равна 1) — это возможно.
|
Линия рынка капитала. |
Портфели, которые лежат на этой прямой, называются лежащими на линии рынка капитала ( CML — Capital Market Line) и они количественно преобладают над портфелями, лежащими на эффективной границе, — инвесторы предпочитают такие портфели всем другим. Добавим, что инвесторы не компенсируют убытков от нерыночного риска, поскольку оптимальные портфели лежат на CML. Эта модель также утверждает, что активы с более высоким риском должны иметь более высокие прибыли. Так как риск теперь отнесен к рыночному портфелю, используется линейная мера чувствительно — Сти риска ценной бумаги к рыночному риску. Эта линейная мера носит название бета.
Рациональный инвестор будет стремиться минимизировать свой риск и увеличить доходность, поэтому всем возможным портфелям, представленным на рис. 16, он предпочтет только те, которые расположены на отрезке ДЕ и составляют эффективную границу множества. Это объясняется тем, что портфели на кривой ДЕ являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью.
Портфель Марковица
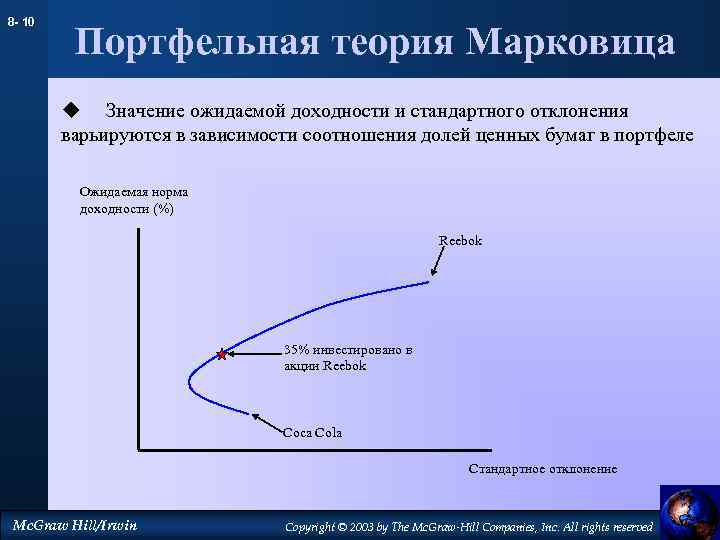
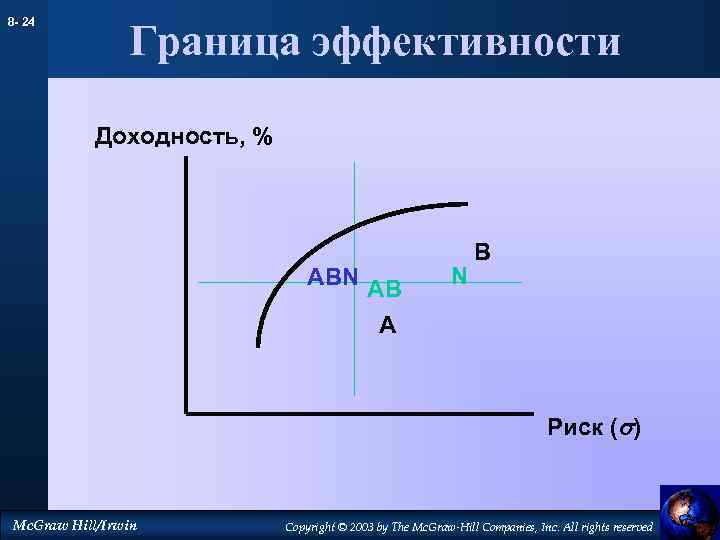
Подход Марковица предполагает, что в портфеле не могут находиться короткие позиции по инструментам, т.е. спекулятивная составляющая в нём полностью отсутствует. Кроме того, доходность портфеля не может превышать максимальную из доходностей составляющих его инструментов. Грамотно составленный портфель должен быть сбалансирован с точки зрения доходности и риска таким образом, чтобы в идеале стремиться к непрерывному росту, хотя отдельные его составляющие могут временно терять в цене. Наиболее оптимальные комбинации инструментов образуют множество, называемые эффективными портфелями. Их ещё называют не улучшаемыми: для каждого из них невозможно добиться повышения доходности без одновременного повышения риска.
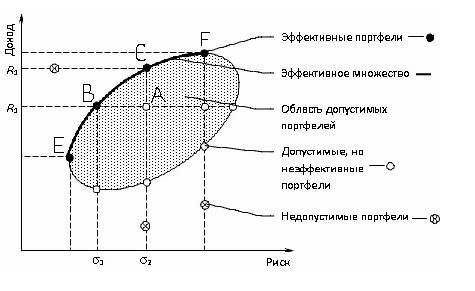
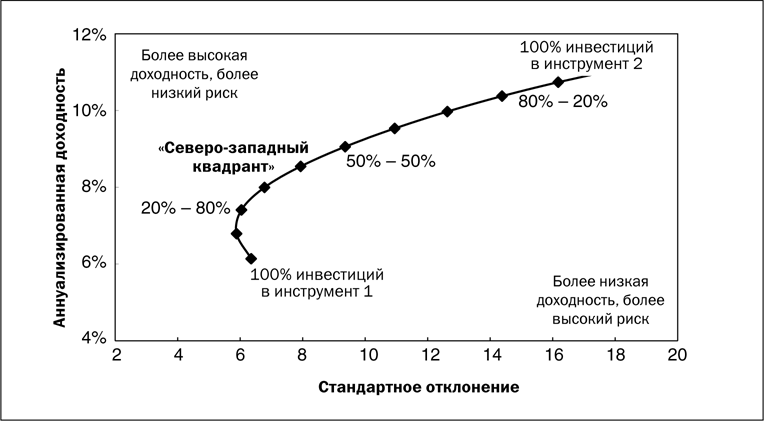
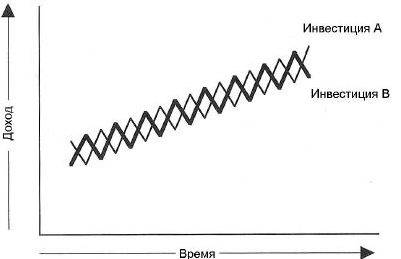
На этом графике кривая эффективных портфелей показывает максимально сбалансированные комбинации инструментов. Эту кривую отличает то, что приращение доходности больше, чем соответствующее ему приращение риска. Например, инструмент В имеет большую доходность по сравнению с инструментом Е, но и больший риск. В то же время, инструмент А при той же доходности, что и В, имеет ещё более высокое значение риска. Отсюда видно, что формирование портфеля на основе инструментов Е и В предпочтительнее, чем, например, Е и А или В и А. Кривая допустимых, но неэффективных портфелей отличается от кривой эффективных портфелей тем, что приращение риска, наоборот, больше приращения доходности. Тем не менее, и такие портфели можно рассматривать в качестве вариантов. Все портфели, находящиеся между указанными кривыми, попадают в множество допустимых портфелей. За пределами этого множества оказываются все остальные комбинации, образующие множество недопустимых портфелей. Они исключаются из рассмотрения.
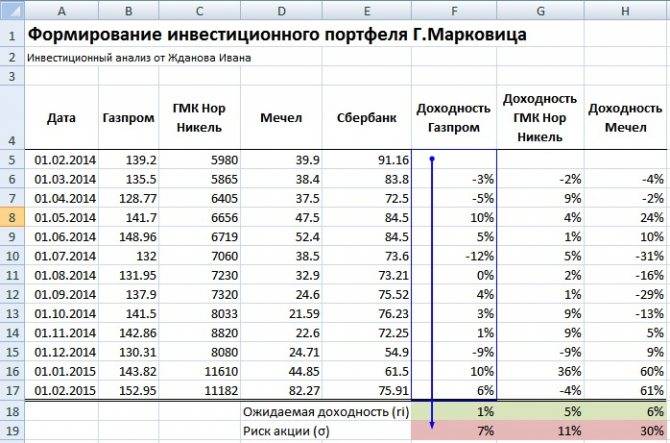
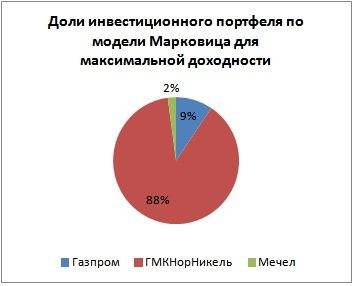
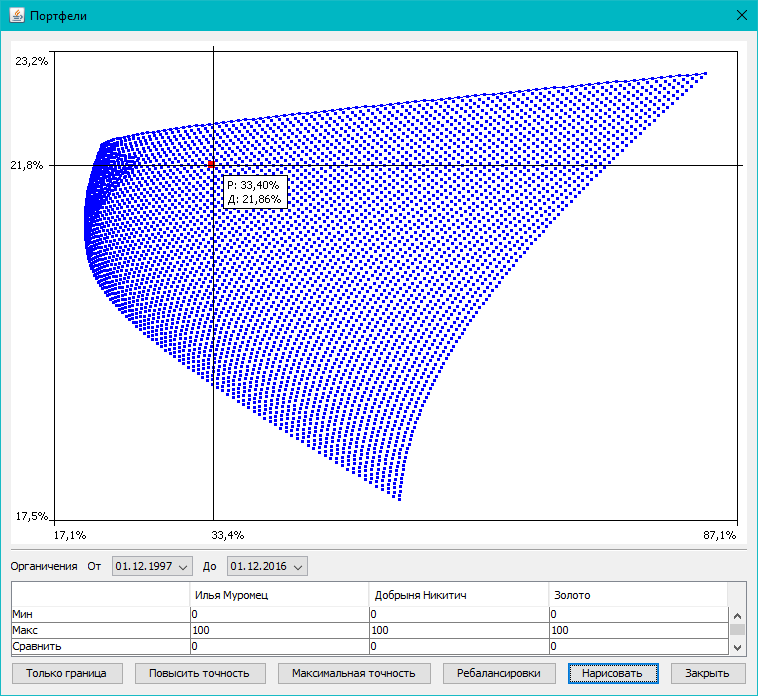
Давайте теперь посмотрим, как можно пользоваться портфельной теорией Марковица на практике. В качестве примера можно взять сервис подбора портфеля на сайте «Сбербанк CIB» (sberbank-cib.ru/products/gm/it/instruments/optimal_portfolio.wbp). Это закрытое акционерное общество, созданное после покупки «Сбербанком» инвестиционной компании «Тройка Диалог». Вначале нужно выбрать ценные бумаги:
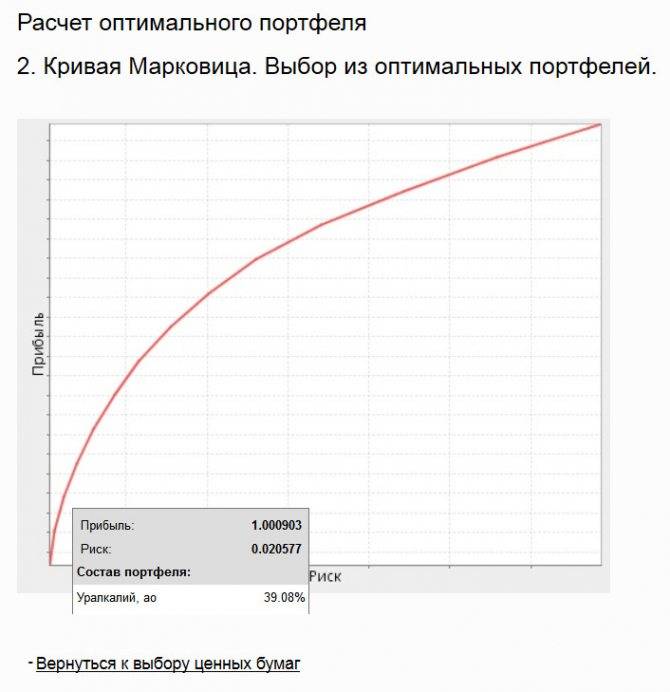
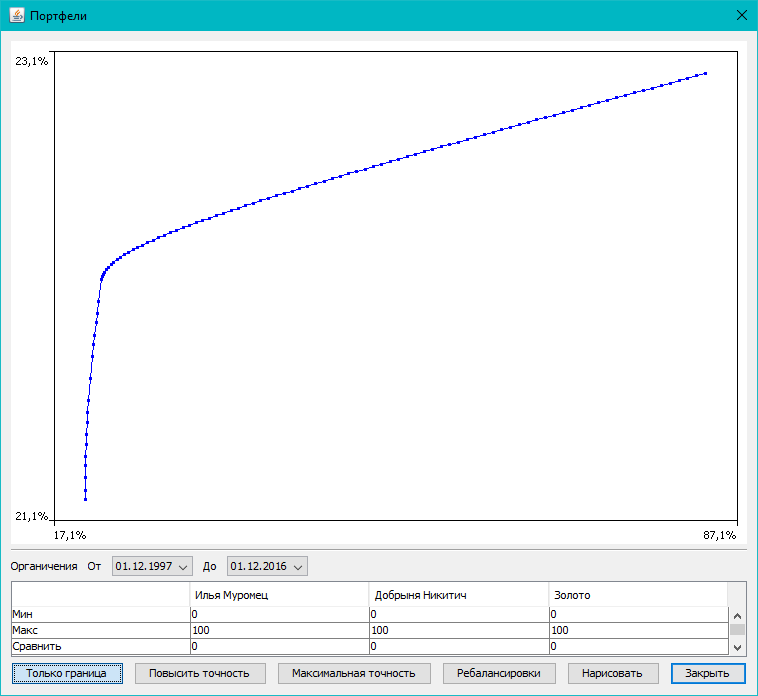
При нажатии на кнопку «Построить кривую Марковица» получаем график риск-доходность:
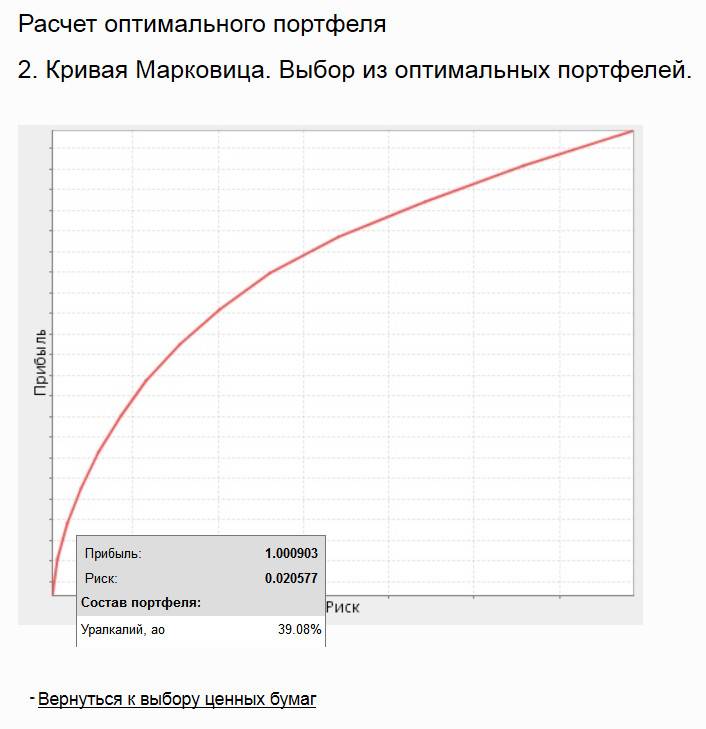
В данном случае кривая эффективных портфелей получается при доле бумаг АО «Уралкалий» в портфеле, равной 39,08%.
Математическая формулировка и решение задач
Портфель Марковица минимального риска
Задача оптимизации портфеля активов с вектором средней доходности r {\displaystyle r} ковариационной матрицей V {\displaystyle V} может быть сформулирована следующим образом
{ σ p 2 = d T V d → min d T r = r p d T e = 1 {\displaystyle {\begin{cases}\sigma _{p}^{2}=d^{T}Vd\rightarrow \min \\d^{T}r=r_{p}\\d^{T}e=1\\\end{cases}}}
К этим условиям в задаче оптимизации портфеля активов следует добавить условие положительности портфеля (долей). Однако, в общем случае финансовых инструментов предполагается возможность открытия коротких позиций (отрицательных долей инструментов в портфеле). Тогда можно найти общее аналитическое решение задачи. Если обозначить,
A = ( r T e T ) V − 1 ( r , e ) = ( r T V − 1 r r T V − 1 e e T V − 1 r e T V − 1 e ) = ( a 11 a 12 a 21 a 22 ) {\displaystyle A={\begin{pmatrix}r^{T}\\e^{T}\\\end{pmatrix}}V^{-1}(r,e)={\begin{pmatrix}r^{T}V^{-1}r&r^{T}V^{-1}e\\e^{T}V^{-1}r&e^{T}V^{-1}e\\\end{pmatrix}}={\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{pmatrix}}}
то решение задачи имеет вид
d ∗ = V − 1 ( r , e ) A − 1 ( r p 1 ) {\displaystyle d^{*}=V^{-1}(r,e)A^{-1}{\begin{pmatrix}r_{p}\\1\\\end{pmatrix}}}
Тогда зависимость дисперсии оптимизированного (эффективного) портфеля от требуемой доходности будет иметь вид
σ p 2 = ( r p , 1 ) A − 1 ( r p 1 ) = a 22 r p 2 − 2 a 12 r p + a 11 a 11 a 22 − a 12 2 = σ 0 2 ( r p − r 0 ) 2 r 0 ( r 1 − r 0 ) + σ 0 2 {\displaystyle \sigma _{p}^{2}=(r_{p},1)A^{-1}{\begin{pmatrix}r_{p}\\1\end{pmatrix}}={\frac {a_{22}r_{p}^{2}-2a_{12}r_{p}+a_{11}}{a_{11}a_{22}-a_{12}^{2}}}=\sigma _{0}^{2}{\frac {(r_{p}-r_{0})^{2}}{r_{0}(r_{1}-r_{0})}}+\sigma _{0}^{2}}
где σ 0 2 = 1 / a 22 , r 0 = a 12 / a 22 {\displaystyle \sigma _{0}^{2}=1/a_{22},r_{0}=a_{12}/a_{22}} — минимально возможная дисперсия доходности портфеля и соответствующая ему средняя доходность
r 1 = a 11 / a 12 {\displaystyle r_{1}=a_{11}/a_{12}} — доходность портфеля, с соотношением риск-доходность таким же как и портфель минимального риска (графически это единственная точка пересечения с параболой прямой, проходящей через начало координат и вершину параболы)
Портфель Тобина минимального риска
При наличии безрискового актива (с нулевой дисперсией доходности) с доходностью r f {\displaystyle r_{f}} формулировка задачи меняется
{ σ p 2 = d T V d → min d T ( r − r f e ) = r p − r f d f = 1 − d T e {\displaystyle {\begin{cases}\sigma _{p}^{2}=d^{T}Vd\rightarrow \min \\d^{T}(r-r_{f}e)=r_{p}-r_{f}\\d_{f}=1-d^{T}e\end{cases}}}
Решение этой задачи имеет вид
d ∗ = r p − r f ( r − r f e ) T V − 1 ( r − r f e ) V − 1 ( r − r f e ) {\displaystyle d^{*}={\frac {r_{p}-r_{f}}{(r-r_{f}e)^{T}V^{-1}(r-r_{f}e)}}V^{-1}(r-r_{f}e)}
Вектор структуры рискового портфеля (доли рисковых активов не во всем портфеле, а в общей стоимости рискового портфеля) будет равен
d ∗ ∗ = V − 1 ( r − r f e ) e T V − 1 ( r − r f e ) {\displaystyle d^{**}={\frac {V^{-1}(r-r_{f}e)}{e^{T}V^{-1}(r-r_{f}e)}}}
Видно, что структура рисковой части портфеля не зависит от требуемой доходности. Требуемая доходность определяет лишь соотношение рискового портфеля и безрискового актива.
Средняя доходность рискового портфеля будет равна
r p ∗ ∗ = r T d ∗ ∗ = r T V − 1 ( r − r f e ) e T V − 1 ( r − r f e ) = a 11 − r f a 12 a 12 − r f a 22 = r 0 ( r 1 − r f ) r 0 − r f {\displaystyle r_{p}^{**}=r^{T}d^{**}={\frac {r^{T}V^{-1}(r-r_{f}e)}{e^{T}V^{-1}(r-r_{f}e)}}={\frac {a_{11}-r_{f}a_{12}}{a_{12}-r_{f}a_{22}}}={\frac {r_{0}(r_{1}-r_{f})}{r_{0}-r_{f}}}}
Стандартное отклонение оптимального (эффективного) портфеля зависит от требуемой доходности линейно, а именно следующим образом
σ p = r p − r f ( r − r f e ) T V − 1 ( r − r f e ) = σ 0 ( r p − r f ) ( r f − r 0 ) 2 − r 0 ( r 1 − r 0 ) {\displaystyle \sigma _{p}={\frac {r_{p}-r_{f}}{\sqrt {(r-r_{f}e)^{T}V^{-1}(r-r_{f}e)}}}={\frac {\sigma _{0}(r_{p}-r_{f})}{\sqrt {(r_{f}-r_{0})^{2}-r_{0}(r_{1}-r_{0})}}}}
Нетрудно также определить связь средней доходности отдельных инструментов со средней доходностью портфеля. Для этого определим вектор коэффициентов
β = V d ∗ σ p 2 = r − r f e r p − r f ⇒ r − r f e = β ( r p − r f ) {\displaystyle \beta ={\frac {Vd^{*}}{\sigma _{p}^{2}}}={\frac {r-r_{f}e}{r_{p}-r_{f}}}\Rightarrow r-r_{f}e=\beta (r_{p}-r_{f})}
Отсюда получаем, что если инвесторы рациональны, то рыночный портфель условно можно считать эффективным, следовательно на рынке средняя доходность инструмента связана с доходностью рыночного портфеля следующим линейным образом
r − r f = β ( r M − r f ) {\displaystyle r-r_{f}=\beta (r_{M}-r_{f})}
Это модель оценки финансовых активов — CAPM
Несколько управленческих моментов
Математик определил, что прирост рисков выше, чем прирост доходности. Кратко говоря о портфельной теория Марковица, стоит сформировать кривые риска и доходности, это достаточно просто сделать на графике — таблице координат, указав значения по каждому инструменту. Теперь легко понять, какой портфель стоит брать в работу в качестве варианта, а какой нет. Если же предложение по числовым значениям не попадает в поле, сформированное кривыми, его лучше не рассматривать.

Некоторые организации, в частности банки или биржевые брокеры на своих сайтах предлагают рассчитать соотношение риска и прибыли согласно формуле в режиме онлайн. Для частного инвестора таких данных о портфельной теории Марковица достаточно, а, чтобы написать курсовую, стоит более детально ее рассматривать и проводить конкретные расчеты
Подводя итог, хочется еще раз уточнить о важности исследования критериев оценки инвестиционного проекта — не только доходности, но суммы вложений, срока работы, рисков, зависимости от рынка
Это позволит заметно сократить минусы, а полученный эффект диверсификации будет замечен более высокой и продолжительной прибылью. Традиционно желаю вам, чтобы полученные знания со статьи или презентации о принципах портфельной теории Марковица помогли определить, куда вложить деньги для получения дохода и минимальными рисками потерь.
Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.
Математика, или не зря мы в школе учились
Я веду этот блог уже более 6 лет. Все это время я регулярно публикую отчеты о результатах моих инвестиций. Сейчас публичный инвестпортфель составляет более 1 000 000 рублей.
Подробнее
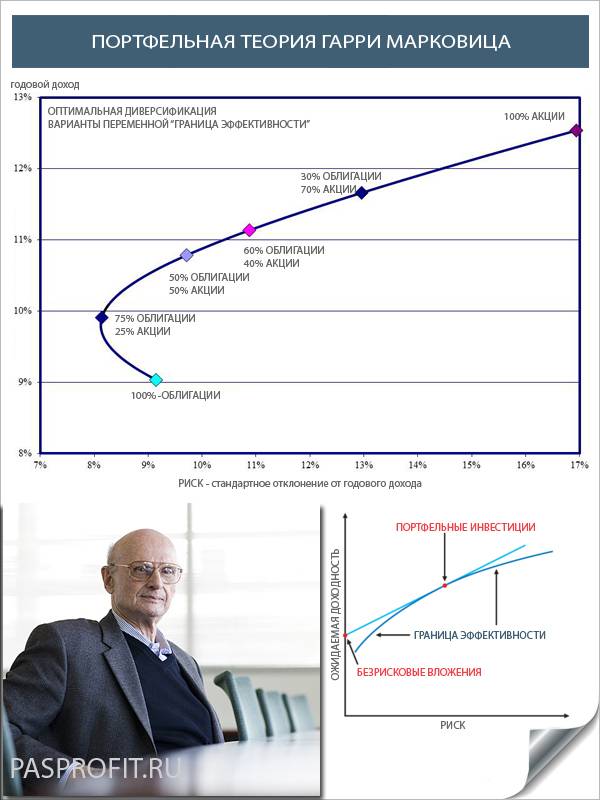
На помощь инвестору приходит математика. Впервые законченную систему создания сбалансированного по доходности и риску портфеля инвестиционных инструментов создал Гарри Марковиц. За эту систему, названную в честь него, Марковиц получил Нобелевскую премию. До сих пор основные правила портфельной теории Марковица применяются банками, инвестиционными компаниями и хедж-фондами. В настоящее время существует немало компьютерных программ, помогающих автоматизировать процесс структурирования портфеля. Тем не менее, понимать базовые принципы этой методики полезно каждому инвестору. Основная идея теории Марковица состоит в том, что доходность инструмента и величина риска связаны между собой. Иными словами, риск является функцией от разброса значений доходности за ряд временных интервалов.

Подбор инструментов для портфеля начинается с оценки математического ожидания доходности каждого инструмента за рассматриваемое время. Это есть среднее арифметическое от доходностей за каждый интервал, а стандартное отклонение от графика доходности – мера риска. Очевидно, что в общем случае, чем выше величина доходности, тем больше по абсолютной величине и разброс значений, а потому и риск. Поясним это на конкретном примере. Пусть доходность за интервал времени имеет следующие значения:
| Период | 1 | 2 | 3 | 4 | 5 |
| Доходность, % | 2 | 3 | 5 | -2 | 4 |
Среднее арифметическое равно (2+3+5-2+4)/5=2,4%
Это и есть ожидаемая доходность. Если инвестиционный портфель состоит из некоторого числа инструментов, то общая ожидаемая доходность портфеля рассчитывается как сумма произведений доходностей отдельных инструментов на их долю в портфеле:
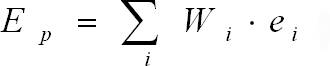
Ep – ожидаемая доходность портфеля; ei – ожидаемая доходность i-го финансового инструмента; wi-доля i-го финансового инструмента в портфеле.
Отклонение доходности инструмента от ожидаемой величины выражается через дисперсию:
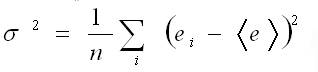
<e>– среднее значение инструмента за весь интервал; n – количество периодов; σ2 – дисперсия доходности инструмента на данном интервале.
Если воспользоваться значениями из таблицы выше, то получаем: ((2-2.4)2+(3-2.4)2+(5-2.4)2+(-2-2.4)2+(4-2.4)2)/5=29.2
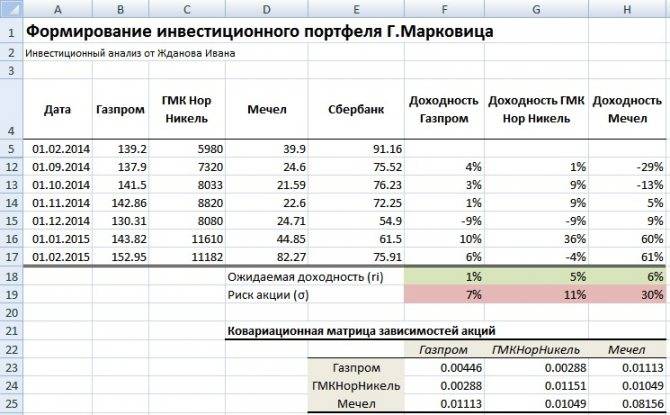
Размерность дисперсии – процент в квадрате, что не очень удобно. Если извлечь из дисперсии квадратный корень, получим стандартное отклонение, что будет мерой риска. В данном случае, это 5.4%. Стандартное отклонение всего портфеля уже невозможно вычислить по такой же простой формуле, как это делалось с доходностью. Приходится вводить новую величину – ковариацию. Она показывает корреляцию между колебаниями величин, каждая из которых случайна. В нашем случае, это доходности рассматриваемых инструментов. Чтобы не усложнять, достаточно лишь упомянуть, что для формирования инвестиционного портфеля предпочтительнее использовать инструменты, колебания доходности которых находятся в разных фазах, т.е. не коррелируют.
Например, это могут быть акции нефтедобывающих и авиакомпаний. В случае падения нефтяных цен акции нефтедобывающих компаний неизбежно будут дешеветь, но в то же время будут дорожать акции авиакомпаний в связи со снижением себестоимости полётов.
Сильные стороны портфельной теории Марковица
- Универсальность. Инвестиционная модель Марковица чаще применяется для формирования оптимальной структуры портфелей ценных бумаг, но подходит и для других видов инвестиционных инструментов – деривативов, опционов, фьючерсов, индексов, объектов недвижимости.
- Вариативность. Помимо определяющих значений допустимого уровня рисков и доходности на эффективность финансовых инструментов оказывают влияние множество факторов, например биржевые показатели, в том числе индекс ммвб. Теория Марковица выявляет не единственный оптимальный, а набор из нескольких вариантов, среди которых инвестор может выбрать удовлетворяющий всем условиям.
- Стабильность. Регулярная переоценка портфеля способствует поддержанию оптимальной структуры активов и значений показателей доходности и риска.
- Низкий уровень риска. Формируемый по принципам Марковица пакет акций не предусматривает торговлю по коротким позициям (спекуляции) или использование заемных средств (кредитного плеча).
Эконометрический вид модели Марковица
Для того чтобы сформировать инвестиционный портфель необходимо решить оптимизационную задачу. Существует два вида задач: поиск долей акций в портфеле для достижения максимальной эффективности при заданном уровне риска (σp) и минимизация риска при заданном уровне доходности портфеля (rp). Помимо этого на уравнения накладываются дополнительные очевидные ограничения: сумма долей активов должна быть равна 1 и сами доли активов должны быть положительными.
В таблице ниже показаны формулы и наложенные на них ограничения для поиска оптимальных долей финансовых инструментов (акций).
| Портфель Марковица минимального риска | Портфель Марковица максимальной эффективности |
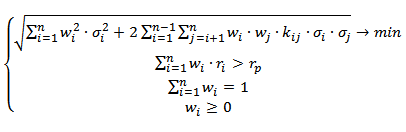 |
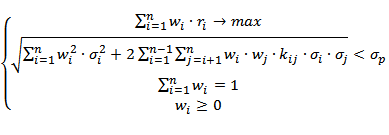 |
| ★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут(расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Минусы методики
Теория Марковица имеет ряд недостатков, выражающихся в следующем:
- невозможность оценить в настоящем времени стандартизированное отклонение с математическим ожиданием, если эти параметры неизвестны на текущий момент;
- оценка стандартизированного отклонения и мат. ожидания с учётом исторических данных возможна только в ближайшей перспективе;
- результаты анализа искомых показателей зависят от глубины исследования истории и могут существенно отличаться в зависимости от рассматриваемого периода.
Проявляется на практике это следующим образом, например, у нас есть компания «А», акции которой до 2015 г демонстрировали показатели, отличающиеся сверхвысоким мат. ожиданием. Однако в период с 2015 до 2018 гг. ситуация стала в корне противоположной, в то время, как рассчитанное среднее значение получается удовлетворительном. Практически это нам не приносит никакой пользы, так как инвестировать в акции компании «А» с учётом текущего положения на основании полученных средних значений крайне нецелесообразно.
Следовательно, прогнозировать перспективы актива по результатам исторических данных невозможно. Разумнее использовать существующие значения и сделать анализ деятельности эмитента с учётом текущих экономических показателей, в большей степени, позволяющих оценить долгосрочные перспективы рынка.
Марковиц разработал свою теорию исключительно для акций, а это рисковый актив, долгосрочные перспективы которого можно оценить только посредством трудоёмкого и дорогостоящего фундаментального анализа финансового рынка, расходы на который сопоставимы с доходами, получаемыми держателями ценных бумаг.
Центральная проблема этой методики заключается в том, что инвестор должен выбрать оптимальный портфель, у которого самый высокий уровень ожидаемого дохода при фиксированных или минимальных рисках. Однако доходность активов, участвующих в рыночных торгах это случайная величина. Сравнивая предполагаемый уровень доходности и его стандартное отклонение, выбирают лучший портфель, руководствуясь не трезвым расчётом, а интуицией.
Эффективный портфель по Марковицу
Все теоретические выкладки, приведенные выше, заимствованы нами из теории эффективности портфеля ценных бумаг Гарри Марковица.
Именно ему принадлежит честь первой (1951 г.) математической формулировки основной задачи, туманящей мозг инвесторам: определения структуры портфеля, которая при известном уровне доходности характеризовалась бы минимальным инвестиционным риском.
Если опираться на нашу диаграмму, эффективный портфель – это точка, которая катится по кривой, соответствующей границе эффективных портфелей.
Именно эта кривая отвечает условиям сформулированной выше задачи.
Решение обозначенной задачи в рамках теории Марковица, однако, требует большого объема статистических данных за максимально продолжительный период функционирования фондового рынка, которым могут похвастаться лишь немногие высокоразвитые страны мира (США, Германия, Франция и т.п.). Россия пока «пролетает» мимо этого списка…
Между тем, применение изложенных в статье методов для оценки эффективности портфелей ценных бумаг с каждым годом становится более обоснованным.
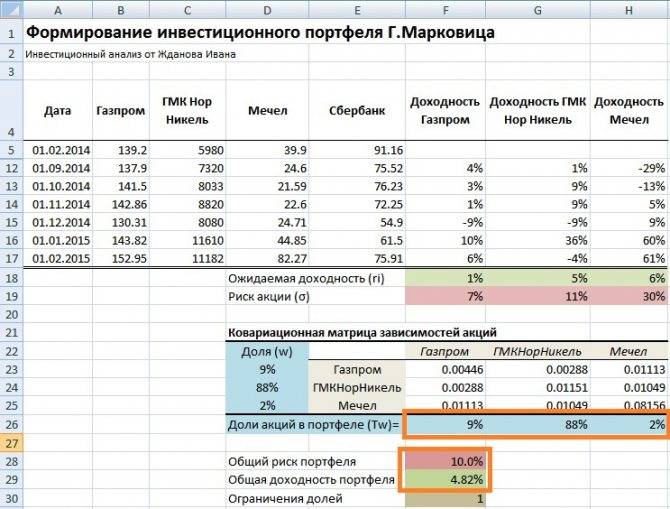
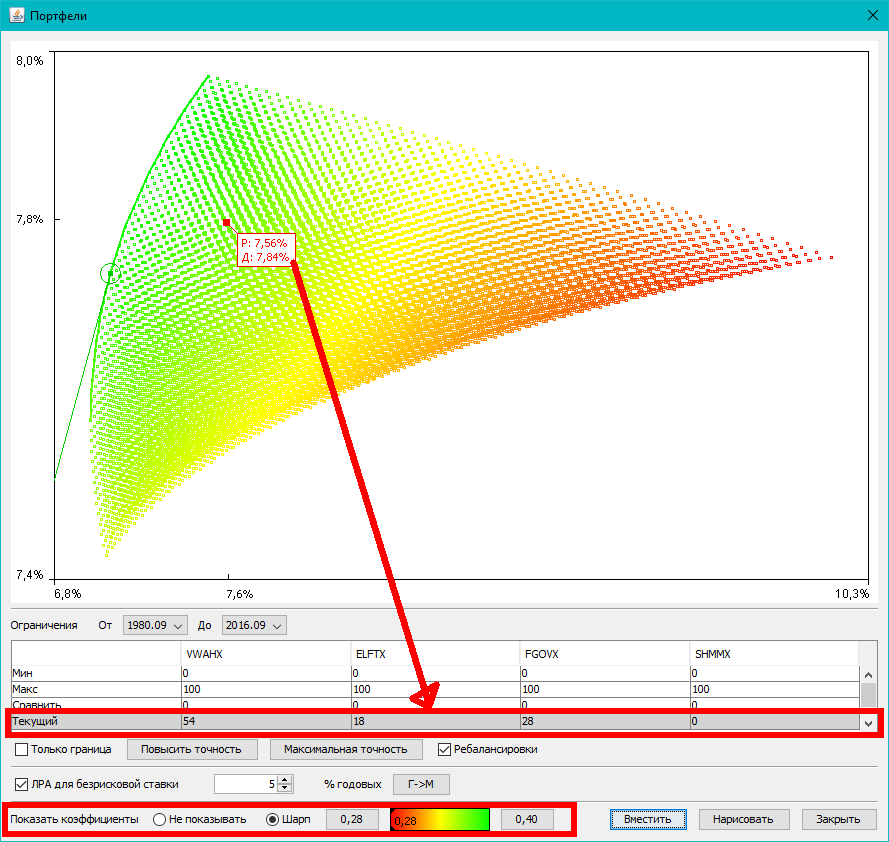
Портфель Марковица через поиск решений (solver) в excel
На этом примере вы поймете как легко рассчитывать портфель Марковица при помощи функции поиск решений (solver) в excel.
Вы можете найти максимальную доходность портфеля при заданном уровне риска или наоборот — риск при заданном уровне доходности. Вы также можете запретить или разрешить короткие позиции в портфеле, добавив специальные ограничения в поиске решений (solver).
Этот пример доступен только в формате excel, поскольку иначе расчеты в нем не будут достаточно понятными.
История возникновения
Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.
Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.
Марковиц постоянно занимается усовершенствованием своей теории и в 1959 году выпускает первую посвящённую ей монографию «Выбор портфеля: эффективная диверсификация инвестиций».
В 1990 году, когда Марковицу вручают Нобелевскую премию, выходит книга «Средне-дисперсионный анализ при выборе портфеля и рынка капитала».
Постановка задачи
Начнем с формулировки задачи. Допустим, мы оказались в ситуации, когда нам необходимо продать ценную бумагу.
Нам известна ее первоначальная стоимость (цена, по которой мы ее приобрели), но неизвестна цена продажи, а также размер дивидендов, которые мы рассчитываем получить за период обладания ценной бумагой.
Очевидно, эффективность продажи ценной бумаги будет столь же непредсказуема, как и любая случайная величина.
Обозначим ее Xt. Численное значение этой величины можно рассчитать по формуле:
Xt = (Pt+1 – Pt) / Pt, где
Pt – цена, по которой ценная бумага приобреталась в момент времени t,
Pt+1 – цена ценной бумаги, по которой она была реализована в момент времени t+1.
Ожидаемая эффективность финансовых вложений в ценную бумагу будет зависеть от параметра Xt.
Фактически речь идет о некоторой функции, представляющей собой математическое ожидание наступления события Xt.
Обозначим эту функцию значением m, причем m = U (X).
Портфельная теория Марковица суть
Книга «Портфельная теория Марковица» от автора, который в 90 лет взялся за разработку еще одного научного масштабного труда, имеет достаточно простую и одновременно сложную суть. Доходность способа для вложения денег и риск прямо связаны между собой. Математический метод позволил описать принцип так: риск — это функция от разброса значений прибыли за определенные временные интервалы.
Метод необходим не только частным инвесторам; его используют банки, инвестиционные и хэдж фонды.
Ключевая задача — добиться высокой диверсификации портфеля не только по суммам вложений, но и по времени работы инструмента. Это актуально, даже работая с небольшими суммами. В учебниках для ВУЗов по экономике и финансированию портфельная теория Марковица активно описывается и много времени уделяется ее изучению
Для инвестора же важно самому или с помощью доверительного менеджера понять базовые постулаты — учитывать 2 критерия во время вложений: доходность и риски, сравнить, например, прибыль за 2 разных периода или вовсе найти один, но суперкритерий оценки
Скачав реферат по экономике или финансовому анализу рынка, можно увидеть, что портфельная теория Марковица хоть и эффективна, но требует и знаний, и усердия в расчётах. При этом, стоит понимать, что нужно владеть информацией из рынка, чтобы выбрать правильные стратегии и подобрать пакет акций для вложений. Сегодня такой расчёт, а также упрощенная версия, согласно теории Шарпа, относится к классу иоп — индивидуальной образовательной программы. Знания, как говориться, за плечами не носить и если есть математически проверенный метод уменьшения риска, почему бы его не использовать не только с акциями, но и другими инструментами?
Теория на примере
Если необходимо показать пример, как эффективно работает портфельная теория Марковица, стоит обратить внимание на доходность за определенный период и суммарное время работы. Для простоты восприятия покажу это в виде таблицы
| Временной интервал в месяцах | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Прибыль % | -5 | 5 | 2 | 3 |
Средний показатель дохода равен (-5+5+2+3)/4=1,25. Это суммарная доходность за весь период (у вас могут быть другие значения). Если же (а так грамотно и рационально делать) в портфеле несколько источников, тогда стоит дополнительно провести расчет еще по одной формуле: ∑р (доходность по всему портфелю) представлена как произведение ожидаемой доходности по одному из инструментов и его доли в общем портфеле. Ожидаемая доходность указывается, когда вы покупаете акции на бирже.
Если вы работаете с большим количеством инструментов, тогда можно использовать для простоты расчета введенную формулу в excel, которая поможет согласно портфельной теории Марковица рассчитать: какая доходность в портфеле от сдачи в аренду квартиры, вложений в бизнес, покупки драгоценных металлов или трейдинга криптовалютой. Рассматривая и применяя разные принципы инвестирования, стоит помнить и о доле риска. Согласно работе математика, он рассчитывается как квадратный корень из произведения 1/n, где n — количество периодов и ∑ (среднего значения дохода способа за вычетом одного периода), возведенного в квадрат. Придется вспомнить математические правила возведения в квадрат выражения и порядок проведения действий.
Работают ли школьные знания?
Взглянув на формулы, представляющие комплексную портфельную теорию Марковица, можно немного испугаться, поскольку они сложные. Но понимания, какая позиция за что отвечает, имея данные по ним, смело можно провести расчеты. Будем честны, далеко не все инвесторы таким занимаются, а пользуются интуицией или школьными знаниями (если такая тема преподавалась) или советами наставника (что более эффективно). Фактически, стоит понимать направление работы, чтобы знания работали: если падает цена на золото, то акции ювелирных компаний будут падать, а изделия дешеветь из-за снижения себестоимости металла.
А что, если будут отклонения?
Читая книгу с детально описанной портфельной теорией Марковица, стоит заметить, что сам автор периодически уточняет, что они могут быть. Основной аспект в том, что стоит оценивать исторический сценарий развития, но он повторяется не всегда и не с точной закономерностью. Достаточно вспомнить цены на акции компаний ЮКОС, Фейсбук, Боинг. Отклонения могут быть связаны и с такими аспектами:
- не описанные точки входа и выхода из рынка;
- не предусмотрено использования торгового плеча.
Формируя инвестиционный портфель, можно одновременно использовать несколько теорий, например, дополнительно учитывать коэффициент шарпа, а более делительные рекомендации по формированию стратегии вложения капитала уже на iqmonitor.ru.
Описание теории

Кривая риск/доходность в модели Марковица После проведённой Марковицем формализации, с математической точки зрения задача по формированию оптимального портфеля представляла собой задачу квадратической оптимизации при линейных ограничениях. Этот класс задач, является одним из наиболее изученных классов оптимизационных задач, для которых существует большое число эффективных алгоритмов.
Для построения пространства возможных портфелей Марковиц предложил использовать класс активов, вектор их средних ожидаемых доходностей и матрицу ковариаций.
На основе этих данных строится множество возможных портфелей с различными соотношениями доходность-риск.
Так как в основе анализа лежат два критерия, менеджер выбирает портфели:
- Либо поиском эффективных, или неулучшаемых решений. В этом случае любое другое решение, лучше найденных по одному параметру обязательно будет хуже по другому.
- Либо выбирая главный критерий (например, доходность должна быть не ниже определённой величины) остальные используя лишь в качестве критериальных ограничений.
- Либо задавая некий суперкритерий, который является суперпозицией указанных двух (например, их функцией).