Числа фибоначчи

Числа Фибоначчи в природе

Сам Фибоначчи упоминал эти числа в связи с такой задачей: «Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?». Решением этой задачи и будут числа последовательности, называемой теперь в его честь. Впрочем, описанная Фибоначчи ситуация — больше игра разума, чем реальная природа.

Индийские математики Гопала и Хемачандра упоминали числа этой последовательности в связи с количеством ритмических рисунков, образующихся в результате чередования долгих и кратких слогов в стихах или сильных и слабых долей в музыке. Число таких рисунков, имеющих в целом долей, равно .

Числа Фибоначчи появляются и в работе Кеплера 1611 года, который размышлял о числах, встречающихся в природе (работа «О шестиугольных снежинках»).

Интересен пример растения — тысячелистника, у которого число стеблей (а значит и цветков) всегда есть число Фибоначчи. Причина этого проста: будучи изначально с единственным стеблем, этот стебель затем делится на два, затем от главного стебля ответвляется ещё один, затем первые два стебля снова разветвляются, затем все стебли, кроме двух последних, разветвляются, и так далее. Таким образом, каждый стебель после своего появления «пропускает» одно разветвление, а затем начинает делиться на каждом уровне разветвлений, что и даёт в результате числа Фибоначчи.

Вообще говоря, у многих цветов (например, лилий) число лепестков является тем или иным числом Фибоначчи.

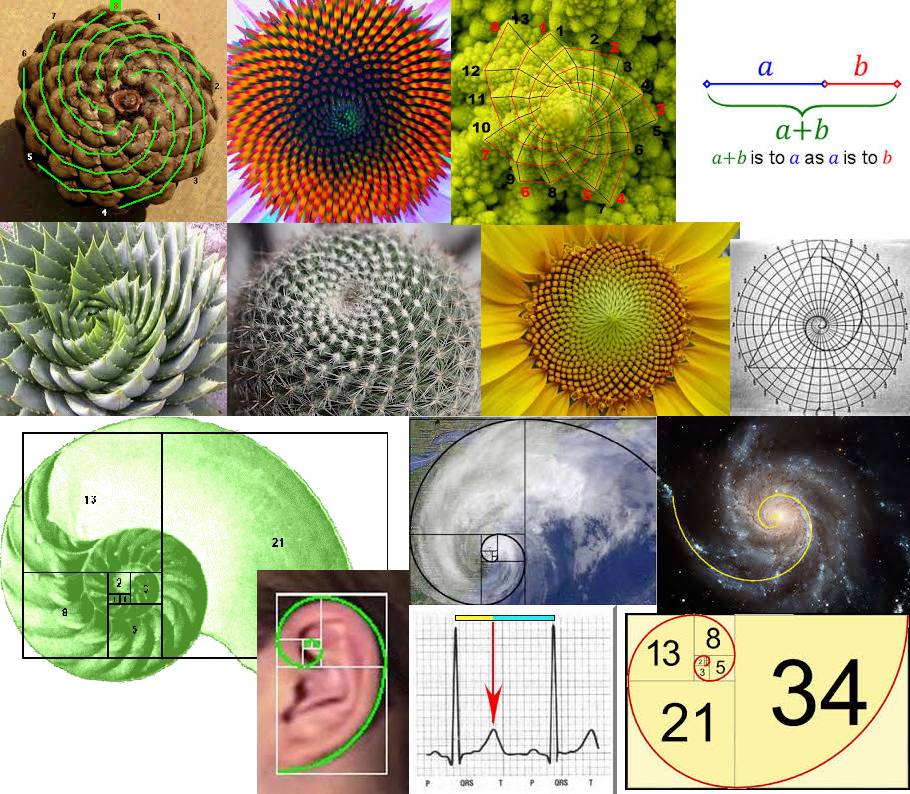
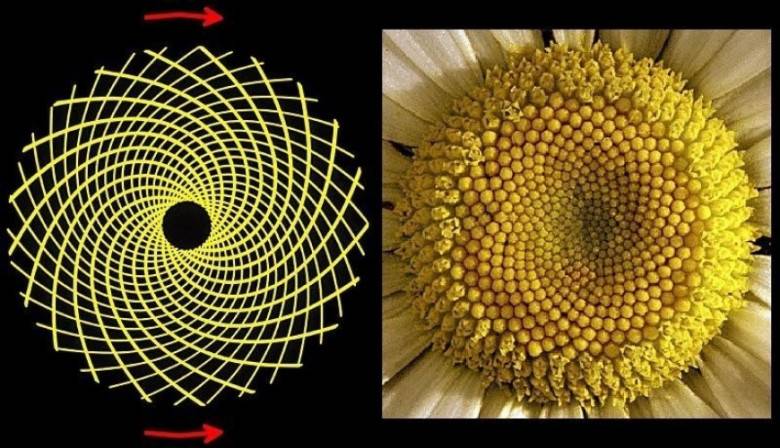
Также в ботанике известно явление »филлотаксиса». В качестве примера можно привести расположение семечек подсолнуха: если посмотреть сверху на их расположение, то можно увидеть одновременно две серии спиралей (как бы наложенных друг на друга): одни закручены по часовой стрелке, другие — против. Оказывается, что число этих спиралей примерно совпадает с двумя последовательными числами Фибоначчи: 34 и 55 или 89 и 144. Аналогичные факты верны и для некоторых других цветов, а также для сосновых шишек, брокколи, ананасов, и т.д.

Для многих растений (по некоторым данным, для 90% из них) верен и такой интересный факт. Рассмотрим какой-нибудь лист, и будем спускаться от него вниз до тех пор, пока не достигнем листа, расположенного на стебле точно так же (т.е. направленного точно в ту же сторону). Попутно будем считать все листья, попадавшиеся нам (т.е. расположенные по высоте между стартовым листом и конечным), но расположенными по-другому. Нумеруя их, мы будем постепенно совершать витки вокруг стебля (поскольку листья расположены на стебле по спирали). В зависимости от того, совершать витки по часовой стрелке или против, будет получаться разное число витков. Но оказывается, что число витков, совершённых нами по часовой стрелке, число витков, совершённых против часовой стрелки, и число встреченных листьев образуют 3 последовательных числа Фибоначчи.

Впрочем, следует отметить, что есть и растения, для которых приведённые выше подсчёты дадут числа из совсем других последовательностей, поэтому нельзя сказать, что явление филлотаксиса является законом, — это скорее занимательная тенденция.

Спираль Фибоначчи и спираль «золотого сечения»

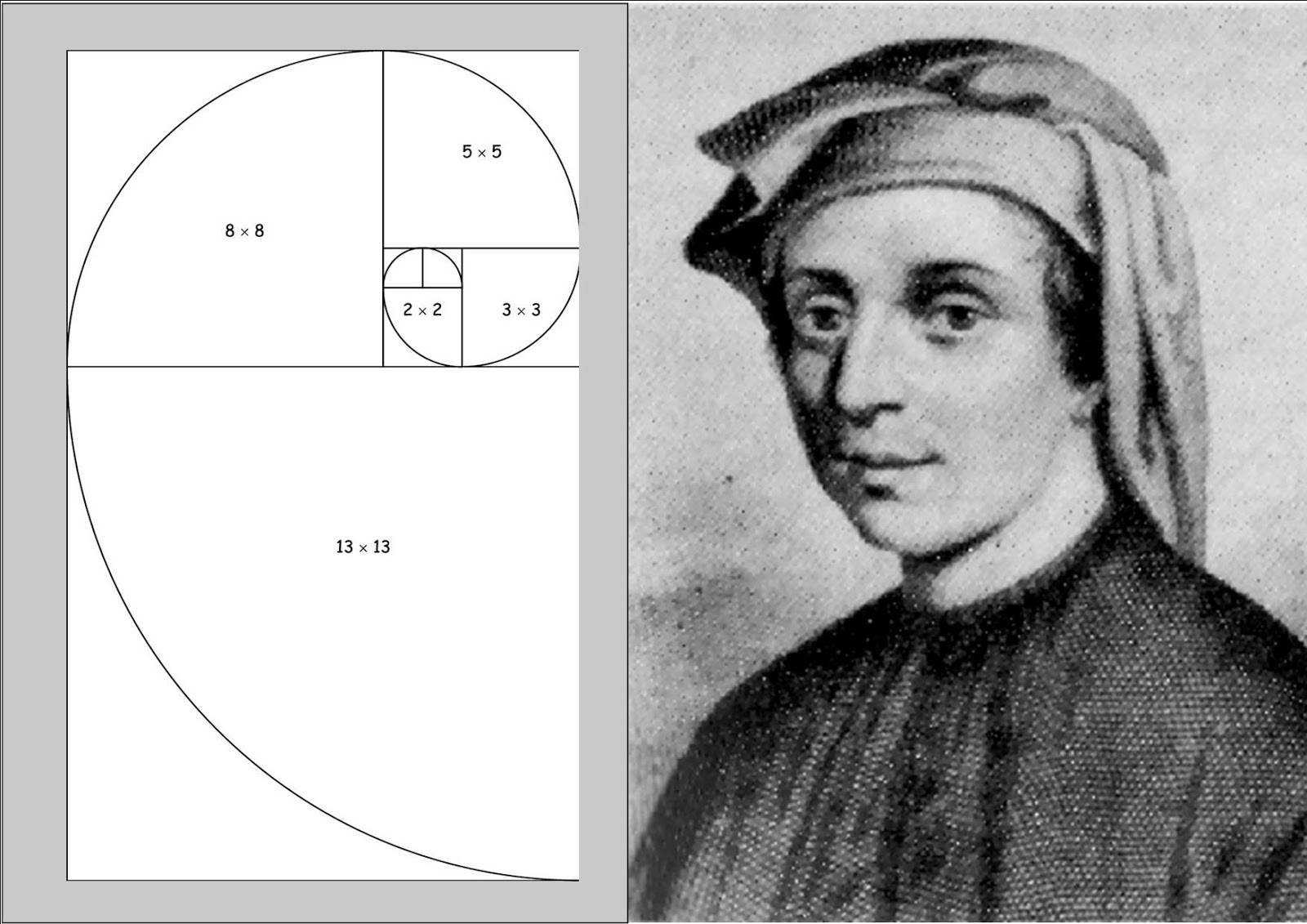
На основе чисел Фибоначчи и «золотого сечения» можно построить спирали. Иногда эти две фигуры отождествляют, но точнее говорить о двух разных спиралях.

Спираль Фибоначчи строят так:

чертят два квадрата (одна сторона общая), длина сторон равна 1 (сантиметр, дюйм или клетка — неважно). Получается поделенный надвое прямоугольник, длинная сторона которого равна 2;
к длинной стороне прямоугольника пририсовывают квадрат со стороной 2

Получается изображение прямоугольника, поделенного на несколько частей. Длинная сторона его равна 3;
процесс продолжают сколь угодно долго. При этом новые квадраты «присоединяют» подряд только по или только против часовой стрелки;
в самом первом квадратике (со стороной 1) чертят от угла до угла четвертинку окружности. Затем без перерыва чертят подобную линию в каждом следующем квадрате.

В итоге получают красивую спираль, радиус которой постоянно и пропорционально увеличивается.

Спираль «золотого сечения» рисуют наоборот:

строят «золотой прямоугольник», стороны которого соотносятся в одноименной пропорции;
выделяют внутри прямоугольника квадрат, стороны которого равны короткой стороне «золотого прямоугольника»;
при этом внутри большого прямоугольника окажется квадрат и прямоугольник поменьше. Тот, в свою очередь, тоже окажется «золотым»;
малый прямоугольник делят по тому же принципу;
процесс продолжают сколь угодно долго, располагая каждый новый квадрат спиралеообразно;
внутри квадратиков рисуют соединенные между собой четверти окружности.

Так получается логарифмическая спираль, которая растет в соответствии с золотым сечением.

Спираль Фибоначчи и «золотая» очень похожи. Но есть главное отличие: у фигуры, построенной по последовательности пизанского математика, есть начальная точка, хотя конечной — нет. А вот «золотая» спираль закручивается «внутрь» до бесконечно малых чисел, как и раскручивается «во вне» до бесконечно больших.

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

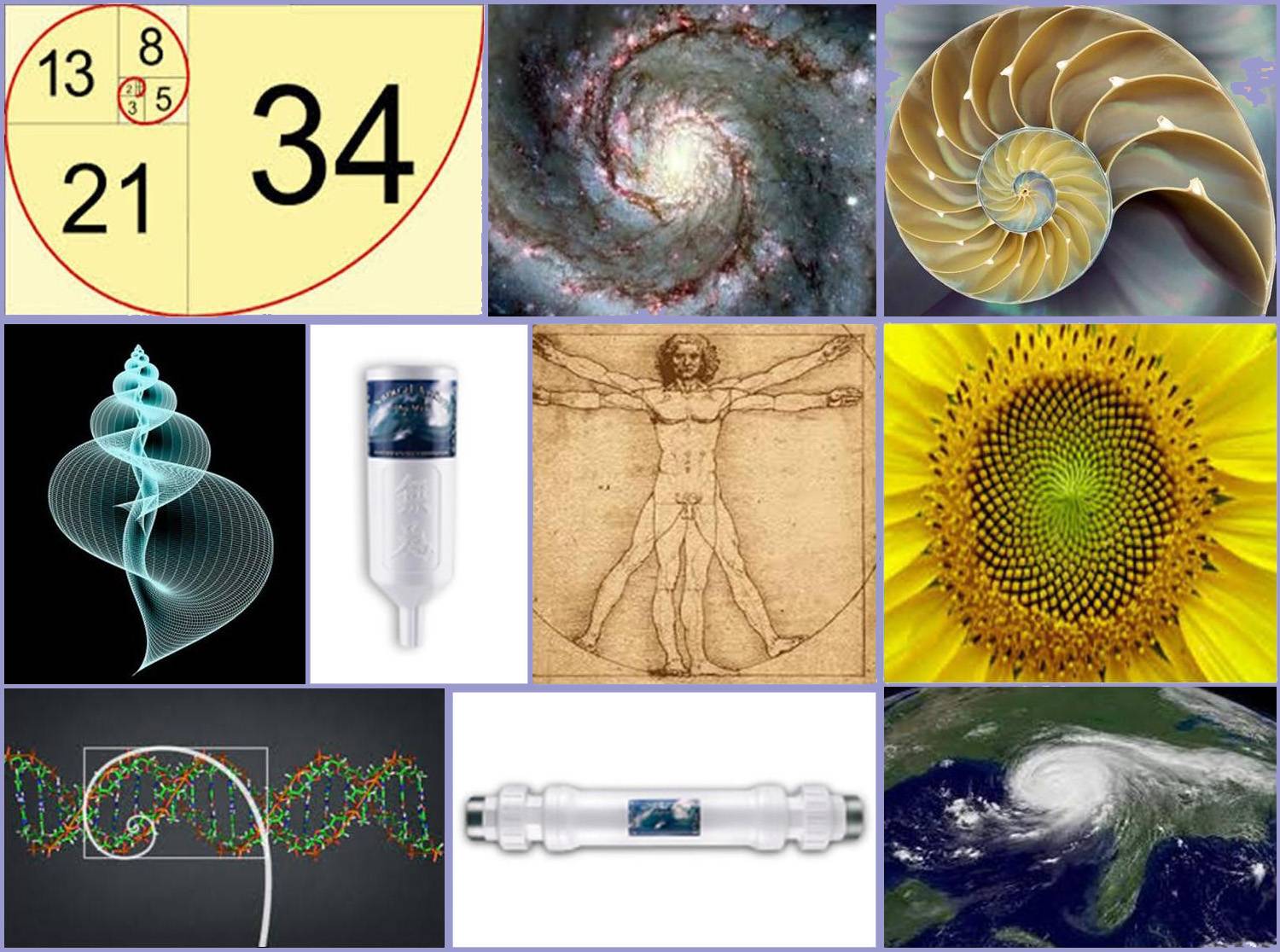
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет

Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

https://youtube.com/watch?v=c3SVIQBXMnA

Как появились числа и их производные

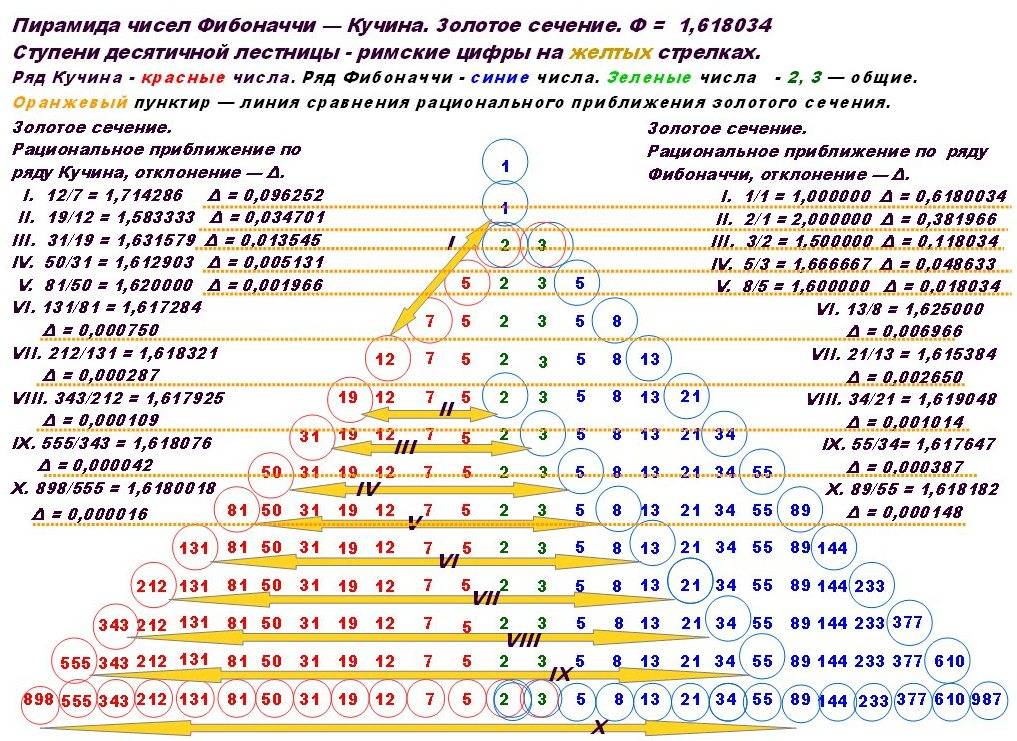
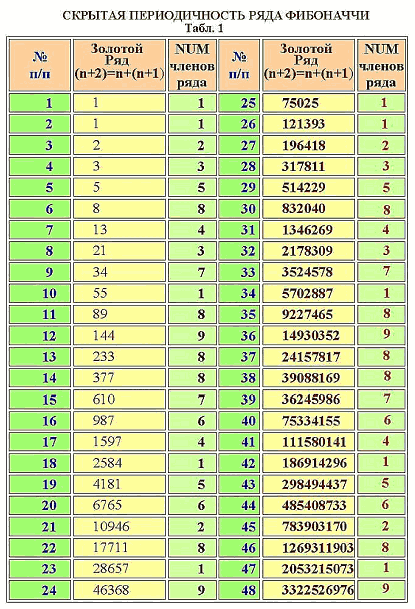
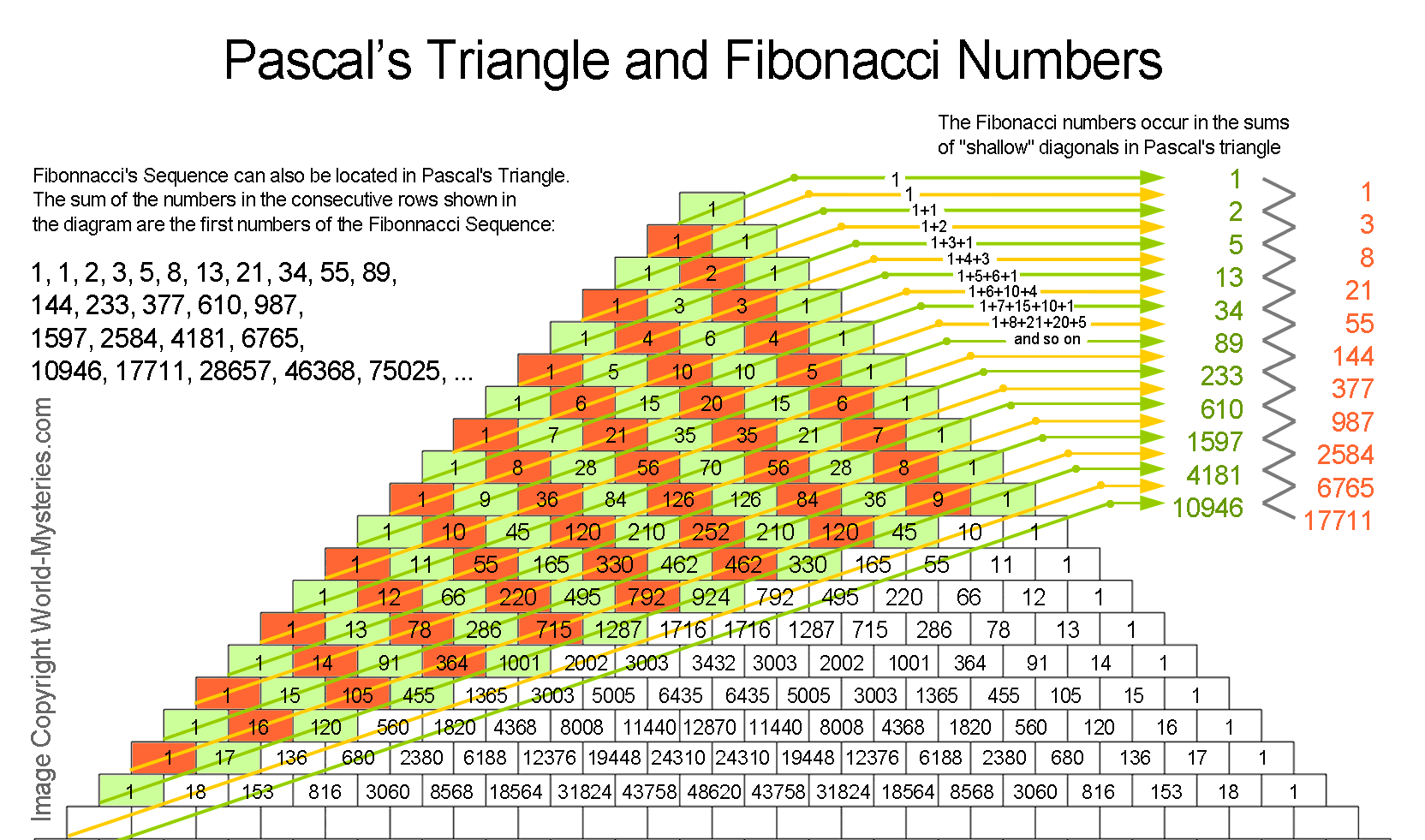
Решая прикладную задачу, Леонардо наткнулся на любопытный ряд чисел Фибоначчи, вначале которого находятся две единицы.

Каждый последующий член – это сумма двух предыдущих. Самое любопытное, что числовой ряд Фибоначчи – примечательная последовательность тем, что если любой член поделить на предыдущий, то получится число, которое близко к 0,618. Этому числу дали имя «Золотое сечение».

Оказалось, что это число было известно человечеству очень давно. Например, в древнем Египте строили пирамиды с его использованием, а древние греки возводили по нему свои храмы. Леонардо да Винчи показал, как строение тела человека подчиняется этом числу.

Природа применяет числа из ряда Фибоначчи в своих наиболее сокровенных и продвинутых областях. От атомных структур и других мелких форм, как молекулы ДНК и микрокапилляры мозга до огромных, как планетарные орбиты и структуры галактик. Ряд примеров настолько велик, что следует утверждать, что в природе действительно присутствует некий основной закон пропорций.

Поэтому не удивительно, что ряд Фибоначчи и золотое сечение пробралось и на биржевые графики. И не одно число 0,618, но и его производные.

Если число золотого сечения возвести в первую, вторую, третью и четвертую степень и вычесть результат из единицы, то получиться новый ряд, который носит название «коэффициенты коррекции Фибоначчи». Осталось только добавить отметку пять десятых – это пятидесятипроцентная коррекция Чарльза Доу.

Однако, это не все, что можно сделать с золотым сечением. Если единицу разделить на 0,618 то получается 1,618, если возведем в квадрат, то у нас получится 2,618, если возведем в куб, то получим число 4,236. Это коэффициенты расширения Фибоначчи. Тут не хватает только числа 3,236, которое было предложено Джоном Мёрфи.

Стратегия с использованием Фибо

Торговых стратегий на уровнях Фибоначчи великое множество. Рассмотрим вариант под названием Magic Grid. Это простая консервативная стратегия, которая показывает соотношение прибыли к убыткам 56%. Действия трейдера сводятся к тому, чтобы правильно настроить индикаторы и выставить стоп-приказы, ограничивающие убытки и фиксирующие прибыль.

Для работы используются два индикатора Moving average и сетка Фибоначчи. Метод построения скользящих средних простой (simple), и обе применяются к закрытию свечи (close). У одной будет период 100, у другой — 200. Пересечение этих скользящих скажут о сформировавшемся тренде. Стратегия используется на часовом и 4-часовом таймфрейме.

В терминале Metatrader инструмент сетка называется Линии Фибоначчи. Его нужно будет подкорректировать, добавив уровень 76,4. Делается это следующим способом. Кликнуть 2 раза по сетке, после этого она перейдет в активное состояние. Затем правой кнопкой мыши вызвать меню инструмента. Нужно выбрать “Уровни”. На этой вкладке следует добавить новый уровень — 0,764. В графе “Описание” записать 76,4. Затем нужно сохранить изменения.

В стратегии используются 2 сетки. Поэтому лучше каждую из них помечать своим цветом, чтобы не перепутать уровни. Сделать это можно там же в свойствах инструмента.

Рассмотрим, как торговать по уровням Фибоначчи на примере восходящего тренда.

При пересечении быстрой скользящей с периодом 100 медленную скользящую, устанавливаем наличие бычьего тренда.

Следующим этапом нужно дождаться начала коррекции. Это можно определить по нескольким факторам:

Тренд выходит из своего коридора.
Верхушки свечей (high) перестают обновляться.
Нижние тени свечей стремятся обновить предыдущие тени.
Индикаторы RSI, Stochastic могут показывать зону перекупленности.

Нужно построить уровни Фибоначчи, как только началась коррекция тренда. Для этого натягивается сетка № 1 от минимального значения тренда до максимального. Минимум будет точкой “A”, а максимум — точкой “B”.

Как только откат достигнет уровня 38,2 и выше, из точки “B” тянется сетка № 2 в противоположном направлении, то есть в сторону коррекции до ее окончания. Это будет точкой “C”.

Вход в сделку по направлению тренда осуществляется на уровне 76,4 сетки № 2. Первая цель фиксации прибыли устанавливается также по второй сетке на уровне 161,8. Stop loss выставляется ниже точки “C” на несколько пунктов.

В дополнение к этой стратегии можно сказать, что если коррекция не дошла до уровня 38,2, то откат не торгуется. Если цена пробила уровень 76,4, то данная коррекция рассматривается, как медвежий тренд. Точка “В” становится точкой “А”, точка “C” будет точкой”B”. При пробое уровня 76,4, рассматриваются сделки на продажу.

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Исследования золотого сечения в 16-19 веках

Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.

В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.

Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.

Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.

Числа Фибоначчи в природе.

Смотреть

А теперь, давайте поговорим о том, как можно опровергнуть то, что цифровой ряд Фибоначчи причастен к каким-либо закономерностям в природе.

Возьмем любые другие два числа и выстроим последовательность с той же логикой, что и числа Фибоначчи. То есть, следующий член последовательности равен сумме двух предыдущих. Для примера возьмем два числа: 6 и 51. Теперь выстроим последовательность, которую завершим двумя числами 1860 и 3009. Заметим, что при делении этих чисел, мы получаем число близкое золотому сечению.

При этом числа, которые получались при делении других пар уменьшались от первых к последним, что позволяет утверждать, что если этот ряд продолжать бесконечно, то мы получим число равное золотому сечению.

Таким образом, числа Фибоначчи ни чем сами по себе не выделяются. Существует другие последовательности чисел, которых бесконечное множество, что дают в результате тех же операций золотое число фи.

Фибоначчи не был эзотериком. Он не хотел вложить никой мистики в числа, он просто решал обыкновенную задачу о кроликах. И написал последовательность чисел, которые вытекали из его задачи, в первый, второй и другие месяца, сколько будет кроликов после размножения. В течение года он получил ту самую последовательность. И не делал отношений. Никакой золотой пропорции, Божественном отношении речи не шло. Все это было придумано после него в эпоху Возрождения.

Перед математикой достоинства Фибоначчи огромны. Он от арабов перенял систему чисел и доказал её справедливость. Была тяжелая и долгая борьба. От римской системы счисления: тяжелой и неудобной для счета. Она исчезла после французской революции. Никакого отношения именно к золотому сечению Фибоначчи не имеет.

Спиралей бесконечно много, наиболее популярны: спираль натурального логарифма, спираль Архимеда, гиперболическая спираль.

А теперь давайте взглянем на спираль Фибоначчи. Данный кусочно-составной агрегат складывается из нескольких четвертей окружностей. И не является спиралью, как таковой.

Золотое сечение в композиции. Основы композиции — Золотое сечение

Золотое сечение в композиции рисунков в paint.netМатематически «Золотое сечение» можно описать так — отношение целого к большей его части должно равно отношению большей части к меньшей. Проиллюстрируем на примере отрезка.В нашем случае весь отрезок В разделен на две части – большую А и меньшую Б. Тогда, если В/А будет равно А/Б, деление отрезка будет осуществлено по принципу, называемому «Золотое Сечение».Не совсем точно, но близко к «Золотому сечению», например соотношение 2/3 или 5/8

Числа в подобных соотношениях нередко называют «золотыми».Зачем эта информация нам для рисования в paint.net? «Золотое сечение» важно для композиции. Считается, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные

Именно в подобных соотношениях выбирали размеры хостов для своих картин известные художники.Рассмотрим упрощенный вариант построения «Золотого сечения» для композиции рисунка, или правило «Трети». Заключается правило трети в том, что мы мысленно делим кадр, на три части по горизонтали и вертикали и в точках пересечения воображаемых линий, размещаем ключевые и важные детали нашего рисунка или фотоколлажа.Принцип «золотого сечения» можно применять при кадрировании изображения. Так, например, кадр, сформированный по правилу «золотого сечения», из большой фотографии может иметь следующий вид.

Что такое «Золотое сечение», как оно появилось?

Золотое сечение — так называемая «божественная пропорция», просматриваемая в большинстве природных объектов: раковинах моллюсков, листьев дерева, пчелиных сотах, строении цветов, паучьих сетях, теле человека, молекулах ДНК, птичьих яйцах. Также его наблюдают в геометрии египетских пирамид, многих античных скульптурах, полотнах известных художников.

Сама суть «золотой пропорции» — деление целого на две неодинаковых части. Отношение меньшей части к большей, а большей к целому, выглядит как 0,618 к 1,0. Монах Лука Пачоли объяснял это как «божественное триединство»: меньшая часть целого — Сын Божий, большая – Бог-Отец, а целое – Дух Святой. Кто впервые начал применять ее, достоверно неизвестно, но максимально точно описал Леонардо да Винчи. Есть предположение, что хорошие художники, музыканты, архитекторы, другие люди искусства используют золотое сечение интуитивно – ведь так получается красивее.

Частный случай «божественной пропорции» — правило третей. Оно обусловлено зрительным восприятием человека – при взгляде на картинку, глаз «цепляется» в первую очередь за основные четыре точки, находящиеся на пересечении вертикальных линий с горизонтальными, при условии, что рисунок поделен на девять одинаковых фрагментов. Именно в пределах этих точек размещают основные акценты картинки, ее сюжетный центр.

Спираль золотого сечения

К «божественным пропорциям» относится и так называемый ряд Фибоначчи или спираль Фибоначчи. Средневековый математик составил последовательность чисел, следующего вида: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946 и др., где сумма каждых двух чисел, которые следуют друг за другом, начиная со второго, равна третьему. Яркий пример последовательности Фибоначчи – фаланги пальцев человека, соотношение первой ко второй и третьей. Спирали Фибоначчи просматриваются при взгляде сверху на цветок подсолнуха, ананас, шишки. Раковины большинства моллюсков, рога горной козы также соответствуют им.

Проявление закономерности Фибоначчи в лёгких человека

В ходе особого исследования выяснено, что формирование лёгких происходит согласно золотому сечению. Такой неотъемлемый элемент наших лёгких, как бронхи, характеризуется асимметричностью – правый дыхательный канал на порядок короче левого. Такая асимметрия присуща и их ответвлениям. Отношение длин длиннейших и кратчайших бронхов равняется 1,618.

Большинство художников, обычно заранее создают собственные зарисовки, используя тёрки с идеального тела человека. Так Микеланджело и прочие великие художники эпохи Возрождения перед тем, как создавать картину всегда зарисовывал тела с геометрией, которая эквивалентна золотому числовому значению. Помимо того данные соотношения широко используются археологами для восстановления 100-процентного облика туловища по его отдельным фрагментам.

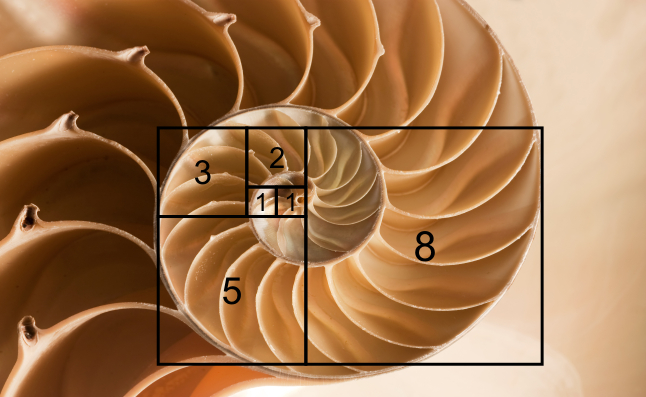
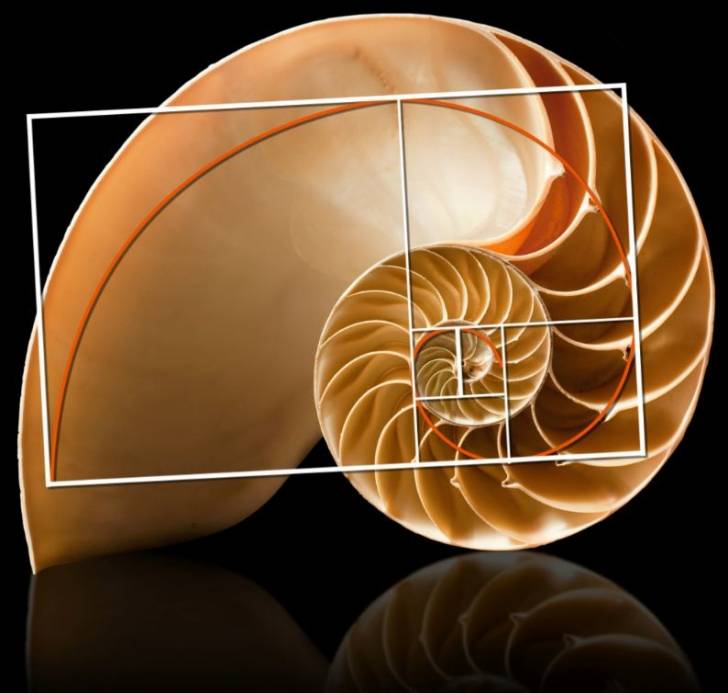
Спираль Фибоначчи – загадка природы (фото)

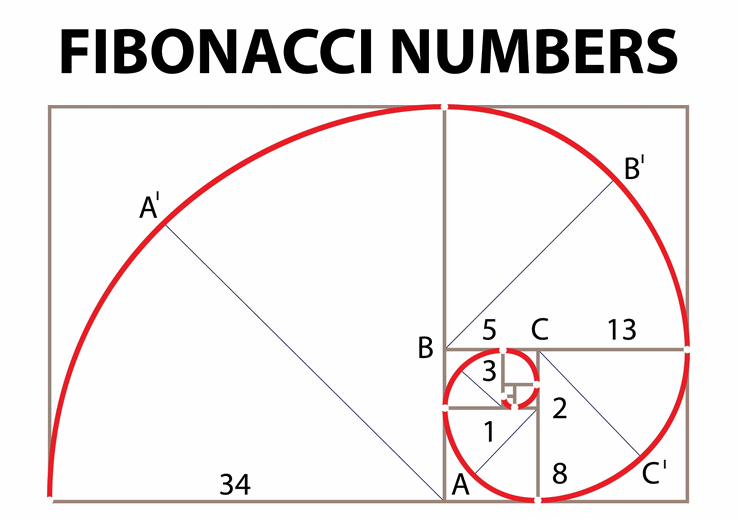
Математические науки не знают второй формы, способной сравниться своими свойствами со спиралью, получившей свои оригинальные свойства благодаря положенному в базис структуры Золотое сечение. Напомним, что формула имеет следующий вид: ( a + b )/ a = a / b.

Известный золотой прямоугольник приобрёл своё название именно в честь того, что он обладает как раз таким соотношением сторон — отношение его длинных сторон к меньшим равно 1,168:1.

Рисунок 4. Спираль Фибоначчи проявляется в природе – это загадка последовательности чисел знаменитого ряда Фибоначчи.

Одним из необыкновенных свойств золотого прямоугольника является то, что если от такой фигуры отделить квадрат, с большей стороной равной длине малой стороны прямоугольника, в результате будет получен ещё один золотой прямоугольник, но меньший по площади.

Причём эту операцию можно повторять постоянно, и каждый раз её итогом будет получение золотого прямоугольника ещё меньшего размера. Интересно, что расположение этих прямоугольников будет соответствовать логарифмической спирали, играющей ключевую роль в математических моделях объектов, которые вполне реально обнаружить в природе.

Обычно спиральную структуру наблюдают в закономерности позиций семян подсолнечника, структуре лепестков некоторых видов цветов, в необычной геометрии ракушек.

У подавляющего большинства улиток раковина обладает именно спиралевидной формой. Поскольку эти существа не обладают разумом, они не могут владеть элементарными математическими знаниями, достаточными для создания собственной раковины подобной формы. Многие учёные не могут точно определить причину, по которой эти моллюски сумели выбрать такую необычную форму существования.

Ясно здесь только, что подобное развитие не может считаться случайным стечением обстоятельств, и сама по себе подобная гипотеза будет выглядеть глупо. Это явно осознанное творение.

Спирали легко обнаружить и в теле человека — к такому примеру можно отнести человеческое ухо, внутренне ухо которого так же включает в себя орган, известный как «Улитка», предназначенный для превращения звуковой вибрации в нейронные сигналы. Схожая с костью, эта структура внутри заполнена жидкостью и внешне напоминает улитку, традиционно соответствующую золотым пропорциям.

Спирали также можно найти на ладонях и пальцах человека, элементарно сняв отпечатки.

В животном мире встретить огромное количество спиралевидных форм можно буквально повсюду — закрученные рога и бивни некоторых видов животных, когти и клювы некоторых видов птиц.

Форму спирали принимает и ураган, и лучше всего это можно наблюдать на снимках, сделанных орбитальной космической станцией, глядя, как скручиваются облака циклона.

В волнах, закручивающихся на морской или океанской глади, ясно виден математический график золотого сечения Фибоначчи в природе со значениями 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55. Не стоит так же забывать о водоворотах, или, по крайней мере, о воде, сливающейся в раковине в водосточную трубу.

Рисунок 5. Загадки спирали Фибоначчи в природе до сих пор не разгаданы.

К слову, золотое сечение угадывается даже в форме галактики.

Спираль заслуженно носит звание «Кривой жизни», ведь её причудливая форма имеет место и угадывается во многих областях. Это настоящий символ эволюции, ибо нет такого объекта, чьё развитие не двигалось бы по спирали.