Ударение в слове симметрию

Симметрии в физике

Основная статья: Симметрия (физика)

Симметрия в физике
Преобразование	Соответствующаяинвариантность	Соответствующийзаконсохранения
Трансляции времени	Однородностьвремени	…энергии
⊠ C, P, CP и T-симметрии	Изотропностьвремени	…чётности
Трансляции пространства	Однородностьпространства	…импульса
↺ Вращения пространства	Изотропностьпространства	…моментаимпульса
⇆ Группа Лоренца (бусты)	ОтносительностьЛоренц-ковариантность	…движенияцентра масс
~ Калибровочное преобразование	Калибровочная инвариантность	…заряда

В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

Суперсимметрия

Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.

По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.

Трансляционная симметрия

Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.

Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.

Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.

При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[уточнить]

Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.

СИММЕТРИЯ

Симметрия — это наиболее очевидный и простой способ достичь композиционного равновесия. Симметрия прослеживается во всем: в природе, в строении человеческого тела, в предметах повседневной жизни.

Не все уравновешенные или сбалансированные фотографии симметричны – все симметричные композиции по умолчанию находятся  в равновесии.

Фото: Robert Biondo

Симметричное равновесие на фотографии достигается тогда, когда объекты с одинаковым визуальным весом будут размещены равноудалённо от центра изображения. Но, создавая такую композицию, необходимо учитывать, что нарушить равновесие может даже небольшой элемент, присутствующий на одной из частей композиции, но отсутствующий на другой. Композиция уже не будет восприниматься симметричной — появится дисбаланс и визуальное напряжение. Происходит это от того, что при восприятии симметрии наш мозг устанавливает определённый ритм объектов и интервалов между ними, предполагает наличие определённой последовательности и интервала. А если этого не происходит — испытывает беспокойство.

Фото: Bramham

В фотографии наиболее часто используются три вида симметрии:

Зеркальная (двусторонняя). Как уже понятно из названия, в основе лежит равенство двух частей композиции, которые расположены по разные стороны центральной оси снимка и являются практически зеркальными отражениями друг друга. Ориентация оси может быть как вертикальная, так и горизонтальная. Симметрию называют чистой, если две половины композиции отражают друг друга абсолютно точно. Но в природе такое встречается достаточно редко, ведь ни для кого не секрет, что даже человеческое тело не полностью симметрично. В большинстве случаев мы имеем дело с неполной симметрией — когда отражения не полностью идентичны и имеют незначительные отличия.

Фото: Hesham Alhumaid

 

 Фото: Stefan Krebs

 

Фото: Bildwerker Freidburg

 

Фото: Davor Plesa

Радиальная (лучевая или круговая). В её основе лежит равное удаление всех элементов композиции относительно центральной точки (или общего центра). Количество объектов, как и угол их расположения относительно центра, могут быть различны. Главное понимать, что пока есть некий общий центр — симметрия сохраняется.

 

Фото: Victor Mozqueda

 

Фото: Markus Studtmann

Трансляционная (кристаллографическая). Это вид симметрии, в которой элементы композиции повторяются через определенные промежутки. Как пример — колонны или окна здания. В трансляционной симметрии ключевую роль играет совпадение направления элементов. С помощи такой симметрии можно создать ритм, движение, показать скорость или очень динамичное действие.

 

Фото: Hans Wolfgang Hawerkamp

 

Фото: Massimo Cuomo

Симметрия в геометрии

Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.

Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию).
Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.

Виды геометрических симметрий:

• Зеркальная симметрия
• Осевая симметрия
• Вращательная симметрия
• Центральная симметрия
• Скользящая симметрия
• Винтовая симметрия

Зеркальная симметрия

Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).

Осевая симметрия

Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.

Вращательная симметрия

Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).

Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.

Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.

В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.

Центральная симметрия

Симметрия относительно точки

Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

Скользящая симметрия

Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).

Двусторонняя симметрия

В двусторонней симметрии (также называется плоскостью симметрии ), только одна плоскость, называется сагиттальной плоскости , делит организм в приблизительно зеркальных изображений половинок. Таким образом , существует приближенная симметрия отражения . Внутренние органы, однако , не обязательно симметричны.

Небольшой император моли, павлиноглазка малая , отображает deimatic модель с двусторонней симметрией.

Животные , которые являются двусторонне симметричными , имеют зеркальную симметрию в сагиттальной плоскости, которая делит тело по вертикали на левую и правую половины, с одним из каждого органа чувств и группы конечностей с обеих сторон. По крайней мере 99% животных являются двусторонне симметричными, включая человека, где симметрия лица влияет суждения людей о привлекательности.

Когда организм обычно двигается в одном направлении, она неизбежно имеет передний или головной конец. Этот конец встречает среду перед остальной частью тела , так как организм двигается, так что сенсорные органы , такие как глаза , как правило, группируются там, а так же это , вероятно , место для рта , как пища встречается. Отличительная голова, с органами чувств , связанных с центральной нервной системой , поэтому (с этой точки зрения) имеет тенденцию к развитию ( цефализации ). Учитывая направление движения , которое создает переднюю / заднюю разницу, и тяжесть , которая создает спинную / вентральную разницу, слева и справа неизбежно отличается, поэтому двусторонне симметричный план тела является широко распространенным и нашел в большинстве типов животных. Двусторонняя симметрия позволяет также рационализацию уменьшить лобовое сопротивление , и на традиционной точке зрения зоологии облегчает передвижение. Тем не менее, в книдарий , существуют различные симметрии, и двустороннюю симметрию, не обязательно совпадает с направлением передвижения, так и другой механизм , такой как внутреннего транспорта могут быть необходимы , чтобы объяснить происхождение двусторонней симметрии у животных.

Морская звезда личинки является двусторонне симметричной , в то время как взрослые имеют .

Филюм иглокожих , который включает в себя морские звезды , морские ежи и доллары песка , является уникальной среди животных , имеющих двустороннюю симметрию на личиночной стадии, но pentamerism ( в пять раз симметрии) , как взрослые.

Двусторонняя симметрия не легко ломаются. В экспериментах с использованием плодовой мушки, дрозофилы , в отличие от других признаков (где лабораторные отбора эксперименты всегда дают изменение), правой или левой односторонности в размерах глаз, или глаз фасета номер, крыловидной складное поведения (оставшиеся справа) шоу отсутствие ответа.

Самки некоторых видов выберите для симметрии, предположительно биологами быть знак (технически «биток») пригодности. Женщина ласточки амбара , вид , где взрослые имеют длинный хвост кос, предпочитают спариваться с самцами , которые имеют наиболее симметричные хвосты.

Цветок пчелиной орхидеи ( офрис пчелоносного ) является симметричен ( зигоморфным ). Губа цветка напоминает (двусторонне симметричное) брюшко самки пчелы; опыление происходит , когда мужчина пчела пытается спариваться с ней.

Цветы в некоторых семействах цветущих растений, такие как орхидеи и гороховых семьи, а также большой частью семейства норичника , являются двусторонне симметричными ( зигоморфным ).

Правописание слова асимметрия

Разобравшись в значении этого слова, можно перейти к правилам грамматики, то есть решить вопрос, как правильно его писать. Они позволят нам разобраться в происхождении этого слова. Чаще всего допускаются ошибки при выборе, какие буквы в этом слове двойные: аССиметрия, асиММетрия или аССиММетрия.

Итак, вспомним, что асимметрия – это противоположность симметрии, ее отсутствие. Само слово симметрия состоит из двух слов: сим-метр. На русский переводится приблизительно, как со-размерность. Двойное «м» здесь обусловлено слиянием двух слов. Следовательно, в слове «асимметрия» есть двойная согласная «м».

Памятуя о том, что оба эти слова пришли к нам от древних греков, а по некоторым источникам, имеет латинские корни, мы без труда вспомним, что приставка «а» означает отрицание. То есть к слову «симметрия» просто прибавляется приставка «а», и получается совершенно новое слово. В обрусевшем варианте асимметрию можно назвать несимметрией. Так мы видим, что в слове не может никак образоваться вторая «с». Ей просто неоткуда взяться.

Как пишется правильно слово «асимметрия», можно прочесть в различных словарях. В них присутствуют некоторые разногласия относительно этимологии этого слова, но принцип правописания везде одинаков. Следовательно, как писать слово «асимметрия», мы разобрались и запомнили.

Оно имеет одну поворотную ось 4-го порядка (ось АВ), четыре поворотные оси 2-го порядка (оси СЕ, DF, MP, NQ), пять плоскостей симметрии (плоскости CDEF, AFBD, ACBE, AMBP, ANBQ).

5. Переносная симметрия

Ещё одним видом симметрии является переносная симметрия.

О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние «а» либо расстояние, кратное этой величине, она совмещается сама с собой Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние «а» — элементарным переносом, периодом или шагом симметрии.

а

Периодически повторяющийся рисунок на длинной ленте называется бордюром. На практике бордюры встречаются в различных видах (настенная роспись, чугунное литье, гипсовые барельефы или керамика). Бордюры применяют маляры и художники при оформлении комнаты. Для выполнения этих орнаментов изготавливают трафарет. Передвигаем трафарет, переворачивая или не переворачивая его, обводим контур, повторяя рисунок, и получается орнамент (наглядная демонстрация).

Бордюр легко построить с помощью трафарета (исходного элемента), сдвигая или переворачивая его и повторяя рисунок. На рисунке изображены трафареты пяти видов: а) несимметричный; б, в) имеющие одну ось симметрии: горизонтальную или вертикальную; г)центрально-симметричный; д) имеющий две оси симметрии: вертикальную и горизонтальную.

Для построения бордюров используют следующие преобразования:

а) параллельный перенос; б) симметрию относительно вертикальной оси; в) центральную симметрию; г) симметрию относительно горизонтальной оси.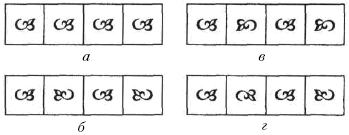

Аналогично можно построить розетки. Для этого круг делят на n равных секторов, в одном из них выполняют образец рисунка и затем последовательно повторяют последний в остальных частях круга, поворачивая рисунок каждый раз на угол 360°/n .

Наглядным примером применения осевой и переносной симметрии может служить забор, изображённый на фотографии.

Вывод: Таким образом, существуют различные виды симметрии, симметричные точки в каждом из этих видов симметрии строятся по определённым законам. В жизни мы повсюду встречаемся тем или иным видом симметрии, а часто у предметов, которые нас окружают, можно отметить сразу несколько видов симметрии. Это создаёт порядок, красоту и совершенство в окружающем нас мире.

ЛИТЕРАТУРА: 

1. Справочник по элементарной математике. М.Я. Выгодский. – Издательство « Наука». – Москва 1971г. – 416стр.

2. Современный словарь иностранных слов. — М.: Русский язык, 1993г.

3. История математики в школе IX — X классы. Г.И. Глейзер. – Издательство «Просвещение». – Москва 1983г. – 351стр.

4. Наглядная геометрия 5 – 6 классы. И.Ф. Шарыгин, Л.Н. Ерганжиева. – Издательство «Дрофа», Москва 2005г. – 189стр.

5. Энциклопедия для детей. Биология. С. Исмаилова. – Издательство «Аванта+». – Москва 1997г. – 704стр.

6. Урманцев Ю.А. Симметрия природы и природа симметрии — М.: Мысль

7. Гильде В.  Зеркальный мир. — М.: Мир, 1982г.

8. Ресурсы сети Интернет.www.likt590.ru/project/matematika/5/, sapr.mgsu.rubiblioarxitektarhkomp2.htm, www.fondcultura.ru/htmls/method/texts_history/architecture.htm, ru.wikipedia.org/wiki/

Радиальная симметрия

Эти актинии были окрашены , чтобы подчеркнуть их радиальную симметрию. ( Плиты из Эрнст Геккель «s Красота форм в природе ).

Симметричные организмы с радиальным напоминают пирог , где несколько режущих плоскостей производить примерно одинаковые куски. Такой организм не проявляет левой или правой стороне. Они имеют верхнюю и нижнюю поверхность, или переднюю и заднюю.

Симметрия является важной исторически в систематике животных; Жорж Кювье классифицированы животные с радиальной симметрией в таксона Radiata ( зоофиты ), который в настоящее время общепринятый быть полифилетической сборкой различных фил от животного царства. Большинство радиально — симметричные животные симметричны относительно оси , проходящей от центра поверхности полости рта, которая содержит рот , к центру противоположного, аборального , конца

Радиальная симметрия особенно подходит для сидячих животных , таких как актинии , плавающих животных , таких как медузы , и медленно движущихся организмов , таких как морские звезды . Животные в фил книдарий и иглокожих радиально симметрично, хотя многие морские анемоны и некоторые кораллы имеют двустороннюю симметрию , определенную единую структуру, в siphonoglyph .

Лилия луковиценосная показывает типичную цветочные симметрию с повторяющимися частямирасположенными вокруг оси цветка.

Многие цветы радиально симметричные или актиноморфные . Примерно одинаковые части цветка — лепестки , чашелистики и тычинки — происходят через регулярные промежутки вокруг оси цветка, который часто является женской частью, с пестиком , стилем и стигмой .

Гастроэнтерит вирусы имеют радиальную симметрию, будучи икосаэдрическим : A  ротавирус , B  аденовирус , C  Norovirus , D  астровирусы .

Многие вирусы имеют радиальные симметрии, их шерсть состоящие из относительно небольшого числа белковых молекул , расположенных в регулярном образце с образованием многогранников, сфер, или окатышей. Большинство из них являются икосаэдры .

Специальные формы радиальной симметрии

Tetramerism представляет собой варианты радиальной симметрии , найденную в медузе , которые имеют четыре каналов в противном случае радиального плана тела .

Apple, вырезать по горизонтали, показывая pentamerism

Pentamerism (также называемый pentaradial и пятиугольная симметрия) означает , что организм состоит из пяти частей вокруг центральной оси, 72 ° друг от друга. Среди животных, только иглокожих , таких как морские звезды , морские ежи и морские лилии являются пятичленные , как взрослые, с пятью лучами , расположенных вокруг рта. Будучи bilaterian животных, однако, они изначально развиваются с зеркальной симметрией , как личинки, а затем получить pentaradial симметрии позже.

Цветущие растения показывают пятикратный симметрию во многих цветах и в различных фруктах. Это хорошо видно в расположении пяти плодолистиков (ботанических фруктов , содержащих семена) в качестве яблока вырезать поперек.

Hexamerism находится в кораллы и актинии (класс Anthozoa ) , которые разделены на две группы в зависимости от их симметрии. Наиболее распространенные кораллы подкласса шестилучевых кораллы имеют гексамерный план тела; их полипы имеют шестикратно внутреннюю симметрию и число их щупалец кратно шести.

Octamerism находится в кораллах подкласса восьмилучевых кораллов . Они имеют полип с восьмью щупальцами и октамерной радиальной симметрией. Осьминога , однако, имеет двустороннюю симметрию, несмотря на восемь рук.

Асимметрия

Асимметрией (др.-греч. ασυμμετρία «несоразмерность» от μετρέω «измеряю») можно считать любое нарушение симметрии. Чаще всего термин употребляется в отношении зрительных объектов и в изобразительном искусстве. В художественном творчестве асимметрия может выступать (и очень часто выступает) в качестве одного из основных средств формообразования (или композиции). Одно из близких понятий в искусстве — аритмия.

В связи с постоянным делением клеток в организме асимметрия в организмах является обычным явлением по крайней мере в одном измерении наравне с биологической симметрией (также см. Межполушарная асимметрия). Луи Пастер полагал, что биологические молекулы асимметричны из-за космических сил, которые осуществляют контроль над их формированием, закладывая свойства (асимметричность), аналогичные своим. Хоть и в его время, и даже сейчас, симметрии в физических процессах придаётся большее значение, так же известны фундаментальные физические асимметрии, начиная с времени.

Существует понятие «преобладающая рука», означающее асимметрию в развитии навыков людей и животных. Тренировка нервных путей во время обучения навыку с одной рукой (лапой) занимает меньше времени, чем та же тренировка с двумя.

Понятие асимметрии существует также в физике (Барионная асимметрия Вселенной, Омическая асимметрия, Ёмкостная асимметрия), математике (Коэффициент асимметрии, Асимметричное отношение, Асимметрический атом, Асимметричная криптография) архитектуре и т. д.

Произношение слов «симметрия», «асимметрия»

Эти лек­се­мы явля­ют­ся тер­ми­на­ми, кото­рые часто упо­треб­ля­ют­ся в мате­ма­ти­ке, физи­ке и дру­гих точ­ных нау­ках. На какой слог пра­виль­но поста­вить уда­ре­ние в этих сло­вах:

«симмЕтрия» или «симметрИя», «асиммЕтрия» или «асимметрИя»?

Чтобы это выяс­нить, раз­де­лим ана­ли­зи­ру­е­мые тер­ми­ны на фоне­ти­че­ские сло­ги в соот­вет­ствии с коли­че­ством глас­ных зву­ков, содер­жа­щих­ся в них:

• си-мме-три-я;
• а-си-мме-три-я.

В про­из­но­ше­нии четы­рех­слож­но­го сло­ва «сим­мет­рия» воз­мож­на поста­нов­ка уда­ре­ния как на вто­рой слог, так и на тре­тий.

Вывод
Согласно орфо­эпи­че­ской нор­ме в сло­ве «сим­мет­рия» пра­виль­но ста­вит­ся уда­ре­ние на глас­ный вто­ро­го сло­га, обо­зна­чен­ный бук­вой «е», и на глас­ный «и» тре­тье­го сло­га.

Правильно ска­жем:

• симме́трия
• симметри́я

В совре­мен­ном рус­ском язы­ке про­из­но­ше­ние про­из­вод­но­го пяти­слож­но­го сло­ва «асим­мет­рия» име­ет толь­ко один пра­виль­ный вари­ант поста­нов­ки уда­ре­ния:

а-си-мме-три́я

Вывод
Согласно орфо­эпи­че­ской нор­ме рус­ско­го лите­ра­тур­но­го язы­ка в сло­ве «асим­мет­рия» пра­виль­но ста­вит­ся уда­ре­ние на глас­ный «и» чет­вер­то­го сло­га.

Согласно утвер­жде­нию авто­ра Л. И. Резниченко «Орфоэпического сло­ва­ря рус­ско­го язы­ка» про­из­но­ше­ние это­го сло­ва с удар­ным глас­ным чет­вер­то­го сло­га (асимме́трия) уста­ре­ло.

Аналогично толь­ко один пра­виль­ный вари­ант уда­ре­ния име­ют слова-термины, закан­чи­ва­ю­щи­е­ся на -ия:

• ветерина́рия
• бюрокра́тия
• гастроно́мия
• рефле́ксия
• флюорогра́фия

Пример. Зеркальная симметрия

Как нужно написать слово РЕАНИМАЦИЯ на капоте машины скорой помощи, чтобы водитель впереди едущей машина увидел в зеркале верную надпись (Рис. 4)?

Рис. 4. Иллюстрация к условию примера

Решение: написать нужно следующим образом (Рис. 5).

Рис. 5. Правильный ответ

Почему так? Потому что в зеркале все видится симметрично (Рис. 6).

Рис. 6. Зеркальная симметрия

Если отразить эту надпись, то в зеркале водитель впереди едущей машины видит РЕАНИМАЦИЯ (Рис. 7). И сразу пропустит такой автомобиль.

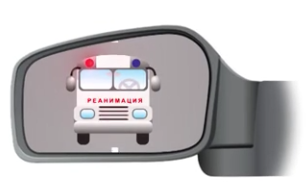
Рис. 7. Как видит надпись водитель впереди едущей машины

Кстати, зеркальная симметрия часто встречается и в природе. Человек, многие животные, рыбы и насекомые практически зеркально симметричны. Почему «практически»? Судите сами на примере человека: строение внутренних органов у человека не симметричное, зато внешне, руки, ноги, глаза, уши и т.д. человек симметричен.

Симметрично ли наше лицо?

Так симметрично ли наше лицо? Сейчас в Интернете можно найти много изображений, которые сделаны так: взята левая половинка лица, которая отражена симметрично направо в компьютерной программе, а потом аналогично с правой. Смотрите, что получается (Рис. 1).

Рис. 1. Слева направо: зеркальное отражение правой половины лица, исходное лицо, зеркальное отражение левой половины лица

Несимметрия животных

Асимметричность в «экстерьере» животных часто выражается в окрасе, что довольно распространено среди кошек, собак и т. д. Это не является отклонением, так как беспородные домашние питомцы несут в себе гены множества различных пород. Однако даже в окрасе животных зачастую встречаются довольно необычные расцветки, которые делают обычную дворняжку совершенно уникальным явлением.

Кроме окраса, животное может страдать отклонениями в пропорциях туловища относительно конечностей. Или одной конечности относительно другой. Это связано с вырождением породы, проявляющемся во внешнем несоответствии требования экстерьера для данной породы. Или возможна разница после травм, которые перенесло животное.

Литература

• Вигнер Е. Этюды о симметрии. — М., Мир, 1971. — 320 с.
• Нокс Р., Голд А. Симметрия в твердом теле. — М., Наука, 1970. — 424 с.
• Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. — М., Наука, 1972. — 340 с.
• Вернадский В. И. Химическое строение биосферы Земли и её окружения. — М., Наука, 1965. — 373 с.
• Болтянский В. Г., Виленкин Н. Я. Симметрия в алгебре. — М., Наука, 1967. — 284 с.
• Под ред. Сенешаль М., Флека Дж. Узоры симметрии. — М., Мир, 1980. — 269 с.
• А. В. Шубников Симметрия и антисимметрия конечных фигур, Изд-во АН СССР, 1951
• И. Харгиттаи, М. Харгиттаи Симметрия глазами химика. — М., Мир, 1989. — 494 с.

Плоскость симметрии

Плоскость симметрии делит кристалл на две зеркально равные части. Обозначается она буквой Р. Части, на которые плоскость симметрии рассекает многогранник, относятся одна к другой, как предмет к своему изображению в зеркале разные кристаллы имеют различное количество плоскостей симметрии, которое ставится перед буквой Р. Наибольшее количество таких плоскостей у природных кристаллов – девять 9Р. В кристалле серы насчитывается 3Р, а у гипса только одна. Значит, в одном кристалле может быть несколько плоскостей симметрии. В некоторых кристаллах плоскость симметрии отсутствует.

Относительно элементов ограничения плоскость симметрии может занимать следующее положение:

1. проходит через ребра;
2. лежать перпендикулярно к ребрам в их серединах;
3. проходить через грань перпендикулярно к ней;
4. пересекать гранные углы в их вершинах.

В кристаллах возможны следующие количества плоскостей симметрии: 9Р, 7Р, 6Р, 5Р, 4Р, 3Р, 2Р, Р, отсутствие плоскости симметрии.

Симметрия в химии

Основная статья: Симметрия молекул

Симметрия важна для химии, так как она объясняет наблюдения в спектроскопии, квантовой химии и кристаллографии.

Кристаллографическая точечная группа симметрии — это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего бесконечного числа точечных групп симметрии только 32 относятся к кристаллографическим.

Анизотропия (от др.-греч. ἄνισος — неравный и τρόπος — направление) — различие свойств среды (например, физических: упругости, электропроводности, теплопроводности, показателя преломления, скорости звука или и др.) в различных направлениях внутри этой среды; в противоположность изотропии. Причиной анизотропности кристаллов является то, что при упорядоченном расположении атомов, молекул или ионов силы взаимодействия между ними и межатомные расстояния (а также некоторые не связанные с ними прямо величины, например, поляризуемость или электропроводность) оказываются неодинаковыми по различным направлениям. Причиной анизотропии молекулярного кристалла может быть также асимметрия его молекул. Макроскопически эта неодинаковость проявляется, как правило, лишь если кристаллическая структура не слишком симметрична.

Симметрия в религиозных сим­во­лах: ряд 1. христианском, иудейском, даосийском; ряд 2. исламском, буд­дий­ском, синтоистском; ряд 3. сикх­ском, в вере Бахаи, индуистском.