проектировать I[править]
Морфологические и синтаксические свойстваправить
| наст. | прош. | повелит. | |
|---|---|---|---|
| Я | проекти́рую | проекти́ровалпроекти́ровала | — |
| Ты | проекти́руешь | проекти́ровалпроекти́ровала | проекти́руй |
| ОнОнаОно | проекти́рует | проекти́ровалпроекти́ровалапроекти́ровало | — |
| Мы | проекти́руем | проекти́ровали | — |
| Вы | проекти́руете | проекти́ровали | проекти́руйте |
| Они | проекти́руют | проекти́ровали | — |
| Пр. действ. наст. | проекти́рующий | ||
| Пр. действ. прош. | проекти́ровавший | ||
| Деепр. наст. | проекти́руя | ||
| Деепр. прош. | проекти́ровав, проекти́ровавши | ||
| Пр. страд. наст. | проекти́руемый | ||
| Будущее | буду/будешь… проекти́ровать |
про-ек-ти́-ро-вать
Глагол, несовершенный вид, переходный, тип спряжения по классификации А. Зализняка — 2a. Соответствующие глаголы совершенного вида — спроектировать, запроектировать.
Корень: -проект-; суффиксы: -ир-ова; глагольное окончание: -ть.
Семантические свойстваправить
Значениеправить
- разрабатывать, составлять проект ◆ Вышедши из государева кабинета, мы с Гирсом проектировали ответную телеграмму графу Шувалову, не давая однако же категорического разрешения до приезда Боголюбова. Д. А. Милютин, Дневник, 1878 г. (цитата из Национального корпуса русского языка, см. ) ◆ Предтеча Леонардо, Дедал, проектирует летательный аппарат. Александр Волков, ««Звездный компьютер» с морского дна» // «Знание — сила», 2010 г. (цитата из Национального корпуса русского языка, см. )
- предполагать, намечать, собираться создать или сделать что-либо ◆ Проектировали даже в честь его по подписке обед, и только по усиленной его же просьбе оставили эту мысль, ― может быть, смекнув наконец, что человека все-таки протащили за нос и что, стало быть, очень-то уж торжествовать нечего. Ф. М. Достоевский, «Бесы», 1871–1872 г. (цитата из Национального корпуса русского языка, см. ) ◆ Мы проектировали наше путешествие так, чтобы сначала запастись здоровьем, а потом уже засесть где-нибудь в немецком городе и провести там зиму. [П. Д. Боборыкин. Жертва вечерняя (1868
Гипонимыправить
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
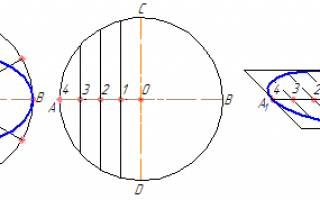
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
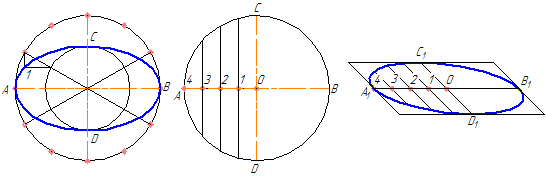 а б вРисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
а б вРисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
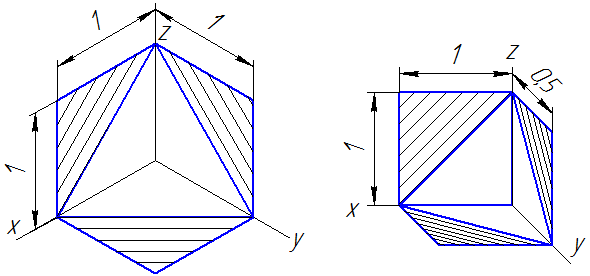 а бРисунок 4.10 – Примеры штриховки в аксонометрических проекциях
а бРисунок 4.10 – Примеры штриховки в аксонометрических проекциях
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.
1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа
1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.
2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.
Убедимся в справедливости последнего утверждения, для чего повернём плоскость π1 в исходное положение (когда π1⊥π2). Для того, чтобы построить точку А необходимо из точек А1 и А2 восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π1и π2, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).
Рисунок 1.8 – Построение эпюра точки
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
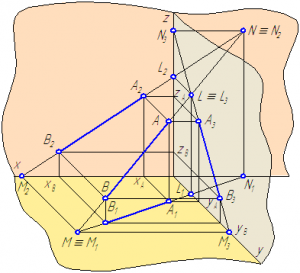
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
A1B1 ∩ xO =N1; YN=0; N ∈ xOz (π2) ⇒ AB ∩ xOz=N
A2B2 ∩ xO =M2; ZM=0; M ∈ xOy (π1) ⇒ AB ∩ xOy=M
A1B1 ∩ yO =L1; XL=0; L ∈ yOz (π3) ⇒ AB ∩ yOz=L
A2B2 ∩ zO =L2;
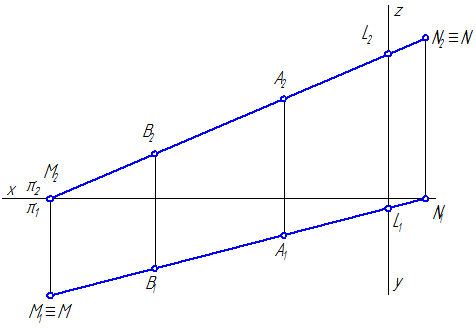 Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ
1.1. Центральное проецирование
Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.
Известны два метода проецирования: центральное и параллельное.
Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).
Рисунок 1.1 – Центральное проецирование
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA, SB – проецирующие прямые (проецирующие лучи).
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
АВСDDDEDE1
Ваша заявка отправленна
В скором времени мы с вами свяжемся
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
\alpha=m\cap n\\\left.\begin{array}{l}a_2\parallel m_2\\a_1\parallel m_1\\\end{array}\right\} \Rightarrow a\parallel\alpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
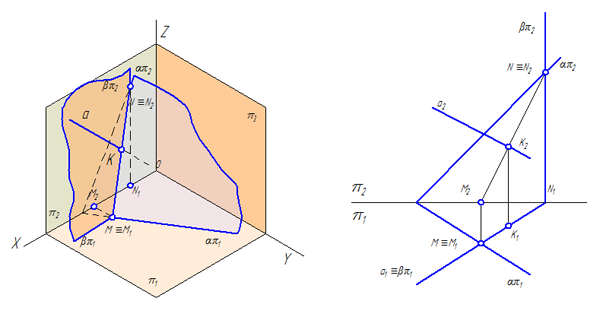
Рисунок 3.13 – Построение точки встречи прямой с плоскостью